The Ultimate Hack To Find The Missing Side Length Of A Right Triangle!

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)

Introduction

Welcome to the fascinating world of right triangles and the ultimate hack to find the missing side length! Whether you're a math enthusiast, a student preparing for exams, or simply someone intrigued by the mysteries of geometry, this article is designed to demystify the process of determining the missing side length of a right triangle.

In the realm of mathematics, right triangles hold a special place due to their unique properties and the profound implications of the Pythagorean theorem. This fundamental concept has captivated mathematicians and learners for centuries, offering a simple yet powerful tool for solving geometric puzzles.

By delving into the intricacies of right triangles and the Pythagorean theorem, you'll uncover the secrets to unlocking the missing side length with ease and confidence. The journey ahead promises to be both enlightening and empowering, as we unravel the enigma of right triangles and equip you with the knowledge to conquer any related challenge.

So, fasten your seatbelt and get ready to embark on a mathematical adventure that will sharpen your problem-solving skills and deepen your understanding of geometric principles. Together, we will navigate through the intricacies of right triangles, unravel the mysteries of the Pythagorean theorem, and emerge with a newfound mastery of finding missing side lengths.

Are you ready to unleash your inner mathematician and unravel the secrets of right triangles? Let's dive in and discover the ultimate hack to find the missing side length of a right triangle!

Understanding Right Triangles

Right triangles are geometric figures that possess unique properties, distinguishing them from other shapes. The defining characteristic of a right triangle is the presence of a right angle, which measures 90 degrees. This fundamental feature creates a sense of balance and symmetry within the triangle, laying the foundation for its remarkable properties.

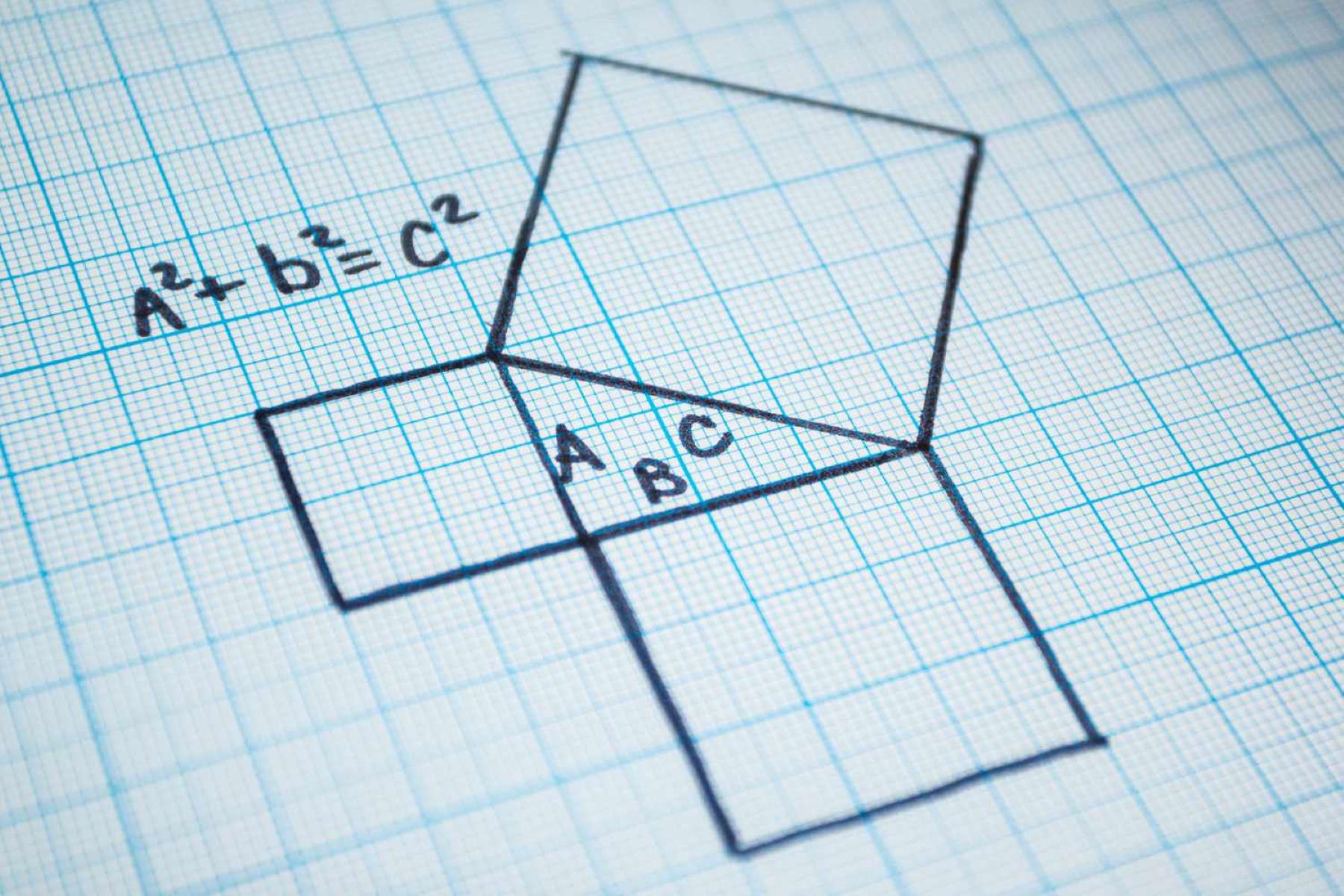
One of the most intriguing aspects of right triangles is the relationship between their sides, known as the Pythagorean theorem. This theorem, formulated by the ancient Greek mathematician Pythagoras, states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This elegant relationship, expressed as a^2 + b^2 = c^2, where 'c' represents the length of the hypotenuse, provides a powerful tool for solving geometric problems and finding missing side lengths.

Furthermore, right triangles exhibit a profound connection between their angles and side lengths, as encapsulated in trigonometric functions such as sine, cosine, and tangent. These functions enable us to relate the angles of a right triangle to the ratios of its side lengths, offering a deeper understanding of the triangle's geometric properties and paving the way for advanced applications in fields such as engineering, physics, and astronomy.

In addition to their mathematical significance, right triangles hold practical relevance in real-world scenarios. Architects and engineers rely on the principles of right triangles to design structures, calculate distances, and determine spatial relationships. Moreover, the concept of similar right triangles forms the basis for trigonometric concepts that are indispensable in navigation, surveying, and various scientific disciplines.

By grasping the essence of right triangles, we gain insight into the elegant interplay between angles and side lengths, the profound implications of the Pythagorean theorem, and the practical applications of these geometric wonders. As we delve deeper into the realm of right triangles, we pave the way for a comprehensive understanding of their properties and unleash the potential to unravel their mysteries with precision and confidence.

The Pythagorean Theorem

The Pythagorean theorem stands as one of the most profound and elegant principles in the realm of mathematics. At its core, this theorem unveils a remarkable relationship between the sides of a right triangle, offering a powerful tool for solving geometric puzzles and unraveling the mysteries of spatial relationships.

Formulated by the ancient Greek mathematician Pythagoras, this theorem asserts that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This fundamental relationship is succinctly expressed as a^2 + b^2 = c^2, where 'c' represents the length of the hypotenuse, while 'a' and 'b' denote the lengths of the other two sides. This elegant expression encapsulates the essence of the Pythagorean theorem, laying the groundwork for a myriad of applications in geometry, trigonometry, and real-world problem-solving.

The implications of the Pythagorean theorem extend far beyond its initial formulation, permeating various branches of mathematics and finding practical utility in diverse fields. By harnessing this theorem, mathematicians and enthusiasts can decipher complex geometric scenarios, determine unknown side lengths of right triangles, and explore the intricate interplay between angles and distances.

Moreover, the Pythagorean theorem serves as a cornerstone for trigonometric concepts, providing a solid foundation for understanding the relationships between angles and side lengths in right triangles. Through its elegant formulation, the theorem unlocks the door to a deeper comprehension of spatial configurations, enabling learners and practitioners to navigate the complexities of geometry with confidence and precision.

In the realm of real-world applications, the Pythagorean theorem finds widespread use in fields such as architecture, engineering, and physics. Its ability to unveil hidden side lengths and establish proportional relationships empowers professionals to design structures, calculate distances, and solve practical problems with ease and accuracy.

As we unravel the intricacies of the Pythagorean theorem, we unveil a timeless principle that transcends the boundaries of mathematics, permeating the fabric of our physical world and empowering us to unravel the mysteries of spatial relationships with clarity and insight. This fundamental theorem stands as a testament to the enduring elegance and practical utility of mathematical principles, serving as a beacon of enlightenment for learners and problem solvers alike.

Using the Pythagorean Theorem to Find the Missing Side Length

The Pythagorean theorem provides a straightforward and reliable method for determining the missing side length of a right triangle. When faced with a right triangle and tasked with finding the length of one of its sides, this theorem serves as a beacon of clarity and precision, guiding us through the intricate interplay of geometric relationships.

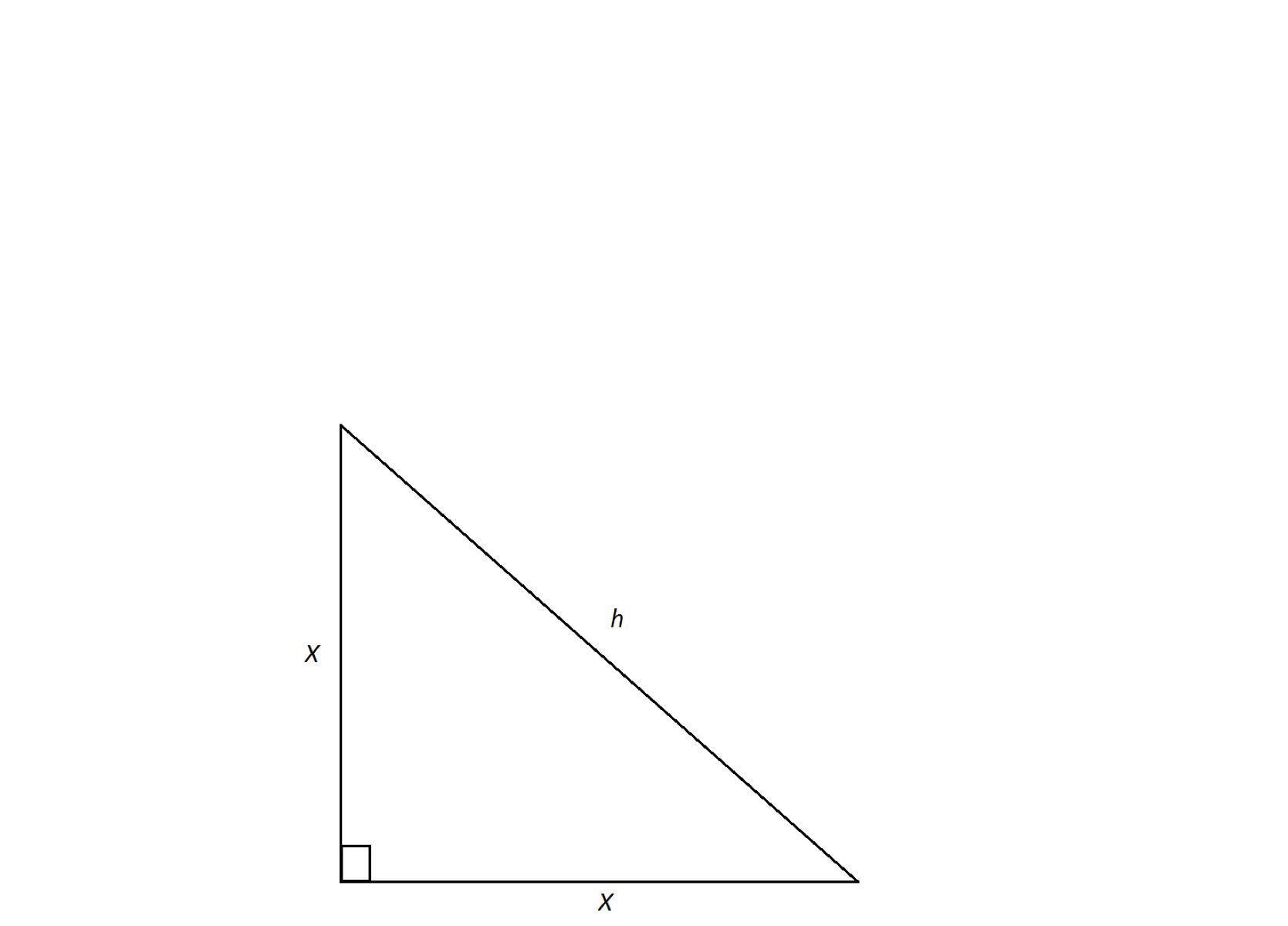
To employ the Pythagorean theorem in finding the missing side length, we first identify the known side lengths of the right triangle. Let's denote these sides as 'a' and 'b', while the unknown side length, which we aim to determine, is represented by 'c'. According to the Pythagorean theorem, the sum of the squares of the two shorter sides is equal to the square of the hypotenuse. This fundamental relationship is expressed as a^2 + b^2 = c^2.

To find the missing side length, we rearrange the equation to solve for 'c', the length of the hypotenuse. By taking the square root of the sum of the squares of the known side lengths, we unveil the precise value of the missing side. This elegant process encapsulates the essence of the Pythagorean theorem, offering a systematic and foolproof approach to unraveling the mysteries of right triangles.

Moreover, the application of the Pythagorean theorem extends beyond mere calculation, as it fosters a deeper understanding of the geometric properties at play. By navigating through the process of determining missing side lengths, learners gain insight into the intricate balance of angles and distances within a right triangle, honing their problem-solving skills and nurturing a profound appreciation for the elegance of mathematical principles.

In real-world scenarios, the ability to find missing side lengths through the Pythagorean theorem holds practical significance, empowering architects, engineers, and problem solvers to tackle spatial challenges with confidence. Whether it's designing a roof truss, calculating the diagonal of a rectangular space, or determining the distance between two points, the Pythagorean theorem stands as a reliable ally, guiding us through the complexities of spatial relationships with precision and clarity.

As we harness the power of the Pythagorean theorem to unveil missing side lengths, we unlock the potential to decipher geometric puzzles, navigate real-world challenges, and deepen our appreciation for the enduring elegance of mathematical principles. This timeless theorem stands as a testament to the timeless beauty and practical utility of mathematical concepts, empowering learners and practitioners to conquer the mysteries of right triangles with unwavering confidence and insight.

Examples of Finding Missing Side Lengths

Let's delve into the practical application of the Pythagorean theorem by exploring real-world examples of finding missing side lengths in right triangles. These scenarios will illustrate the seamless integration of geometric principles and problem-solving techniques, showcasing the elegance and practical utility of the Pythagorean theorem in unraveling spatial mysteries.

Example 1: Roof Truss Design

Imagine you are an aspiring architect tasked with designing a roof truss for a new residential structure. As part of the design process, you need to determine the length of the diagonal beam that will support the roof. By utilizing the Pythagorean theorem, you can effortlessly find the missing side length of the right triangle formed by the horizontal and vertical components of the truss.

Suppose the horizontal beam measures 8 meters, and the vertical beam measures 6 meters. To find the length of the diagonal beam, denoted as 'c', we apply the Pythagorean theorem: a^2 + b^2 = c^2. Plugging in the known side lengths, we calculate 8^2 + 6^2 = c^2, which simplifies to 64 + 36 = c^2. Thus, c^2 = 100, leading to c = √100, yielding a diagonal beam length of 10 meters. With this precise measurement, you can confidently proceed with the roof truss design, showcasing the practical prowess of the Pythagorean theorem in real-world architectural endeavors.

Example 2: Navigational Calculations

In a different scenario, consider a ship captain charting a course across the open sea. To determine the distance between two navigational points, the captain can apply the principles of right triangles and the Pythagorean theorem to find the missing side length, representing the direct distance between the points.

Suppose the ship travels 120 nautical miles eastward and 80 nautical miles northward. By treating the ship's path as the two shorter sides of a right triangle, the captain can ascertain the direct distance traveled, denoted as 'c', using the Pythagorean theorem. Applying the equation a^2 + b^2 = c^2, where a = 120 and b = 80, the captain calculates 120^2 + 80^2 = c^2, leading to 14400 + 6400 = c^2. Hence, c^2 = 20800, resulting in c = √20800, revealing a direct distance of approximately 144.22 nautical miles. Armed with this precise measurement, the captain navigates the open waters with confidence, leveraging the Pythagorean theorem to conquer spatial challenges at sea.

These examples vividly demonstrate the seamless integration of the Pythagorean theorem in practical scenarios, showcasing its ability to unveil missing side lengths and empower problem solvers in diverse fields. Whether in architecture, navigation, or countless other applications, the Pythagorean theorem stands as a timeless ally, guiding us through the complexities of spatial relationships with unwavering precision and clarity.

Conclusion

In conclusion, the journey through the realm of right triangles and the Pythagorean theorem has unveiled a world of geometric wonders, empowering learners and problem solvers to unravel the mysteries of spatial relationships with precision and confidence. By delving into the essence of right triangles, we have gained insight into their unique properties, the profound implications of the Pythagorean theorem, and the practical applications of these timeless principles.

The ultimate hack to find the missing side length of a right triangle lies in the elegant interplay of geometric relationships and the systematic application of the Pythagorean theorem. This fundamental principle, formulated by the ancient mathematician Pythagoras, serves as a beacon of clarity and insight, guiding us through the complexities of spatial puzzles and empowering us to conquer real-world challenges with unwavering precision.

Through the process of employing the Pythagorean theorem to find missing side lengths, we have honed our problem-solving skills, nurtured a deeper appreciation for the elegance of mathematical principles, and discovered the practical utility of geometric concepts in diverse fields. From architectural design to navigational calculations, the Pythagorean theorem stands as a reliable ally, empowering professionals and enthusiasts to navigate the intricacies of spatial relationships with confidence and clarity.

As we reflect on the timeless significance of the Pythagorean theorem, we recognize its enduring impact on mathematics, science, and real-world problem-solving. This fundamental principle transcends the boundaries of theoretical abstraction, permeating the fabric of our physical world and guiding us through the complexities of spatial challenges with unwavering precision.

In essence, the ultimate hack to find the missing side length of a right triangle encapsulates the timeless beauty and practical utility of mathematical principles, empowering learners and practitioners to unravel the mysteries of geometry and navigate the complexities of spatial relationships with confidence and insight. As we embrace the elegance of right triangles and the Pythagorean theorem, we embark on a journey of discovery, enlightenment, and empowerment, equipped with the tools to conquer the mysteries of spatial puzzles and chart a course toward mathematical mastery.