How To Find The Circumcenter Of A Triangle

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)

Introduction

The circumcenter of a triangle holds a significant place in the realm of geometry. It is a point where the perpendicular bisectors of the sides of a triangle intersect. This point plays a crucial role in various geometric and engineering applications, making it a fundamental concept to comprehend.

Understanding the circumcenter of a triangle involves delving into the intricate relationships between the triangle's sides, angles, and vertices. By exploring different methods to locate the circumcenter, we can gain a deeper insight into the geometric properties of triangles and their associated points.

In this article, we will embark on a journey to unravel the mystery of the circumcenter. We will explore multiple techniques to determine this pivotal point, including using perpendicular bisectors, the intersection of angle bisectors, and the coordinates of the triangle's vertices. Each method offers a unique perspective on the concept, providing a comprehensive understanding of how the circumcenter can be identified in various scenarios.

By the end of this exploration, you will have a solid grasp of the significance of the circumcenter and the diverse approaches to pinpointing its location within a triangle. So, let's embark on this geometric adventure and uncover the secrets of the circumcenter!

Understanding the Circumcenter of a Triangle

The circumcenter of a triangle is a point of geometric significance that holds a unique relationship with the triangle's vertices and sides. It is defined as the point where the perpendicular bisectors of the sides of a triangle intersect. This intersection forms the circumcircle, which is a circle that passes through all three vertices of the triangle. The circumcenter is equidistant from the triangle's three vertices, making it a central point of balance within the geometric structure.

One of the most intriguing properties of the circumcenter is its role in determining the stability and symmetry of a triangle. When a triangle is inscribed in a circle, the center of that circle is the circumcenter of the triangle. This connection highlights the circumcenter's pivotal role in defining the spatial relationships between the triangle's elements and the surrounding geometric constructs.

Furthermore, the circumcenter plays a crucial role in various engineering and architectural applications. Its position relative to the triangle's vertices influences the stability and equilibrium of structures, making it a key consideration in design and construction processes. Additionally, the circumcenter serves as a fundamental element in computational geometry, where its coordinates are utilized in algorithms and mathematical models to solve complex geometric problems.

Understanding the circumcenter of a triangle involves delving into the intricate interplay between the triangle's sides, angles, and vertices. By grasping the geometric properties and significance of the circumcenter, we gain valuable insights into the underlying principles of spatial relationships and symmetry within triangles. This understanding forms the foundation for exploring the diverse methods of locating the circumcenter, each offering a unique perspective on this central point's role in the realm of geometry.

As we delve deeper into the exploration of the circumcenter, we will uncover the various methods used to determine its precise location within a triangle. Each method provides a distinct approach to understanding the circumcenter's position, shedding light on its geometric significance and practical applications. Through this exploration, we will gain a comprehensive understanding of the circumcenter's role in the realm of geometry and its broader implications in diverse fields.

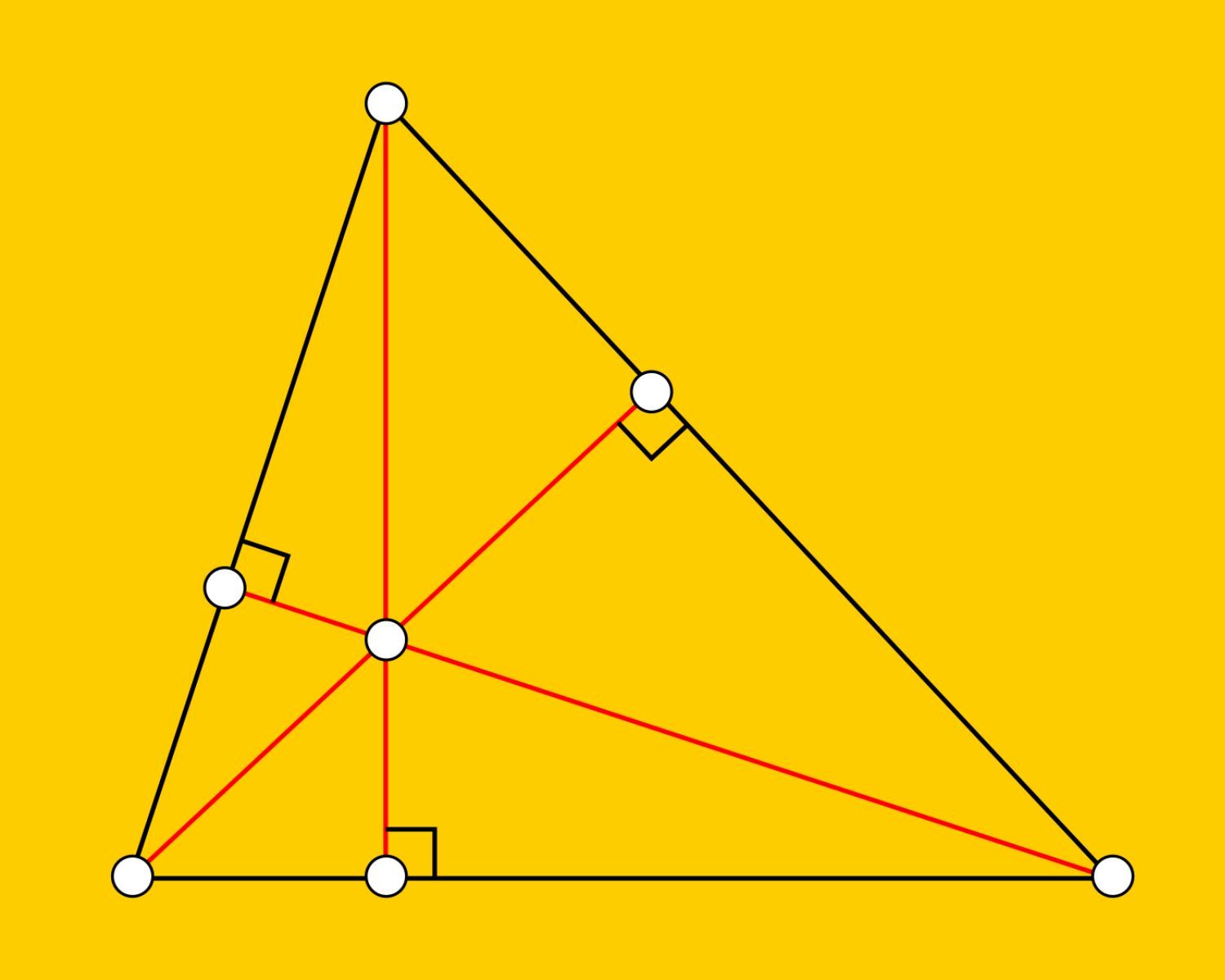
Method 1: Using Perpendicular Bisectors

Using perpendicular bisectors is a fundamental method for locating the circumcenter of a triangle. The perpendicular bisector of a side is a line that intersects the side at a right angle and divides it into two equal segments. To find the circumcenter using this method, we identify the perpendicular bisectors of at least two sides of the triangle and determine their point of intersection.

The process begins by selecting any two sides of the triangle and constructing their respective perpendicular bisectors. These bisectors extend from the midpoint of each side, forming two intersecting lines within the triangle. The point where these lines intersect is the circumcenter of the triangle.

This method leverages the geometric property that the circumcenter is equidistant from the triangle's vertices. The perpendicular bisectors ensure that the distances from the circumcenter to each vertex are equal, forming the basis for the circumcenter's precise location within the triangle.

By employing this approach, we not only determine the circumcenter's coordinates but also gain insights into the spatial relationships between the triangle's elements. The perpendicular bisectors serve as a geometric tool that unveils the symmetrical properties of the triangle, shedding light on its equilibrium and stability.

Furthermore, the use of perpendicular bisectors to locate the circumcenter provides a practical foundation for understanding the concept of concurrency in geometry. The intersection of the perpendicular bisectors signifies a point of concurrency, where the circumcenter harmoniously aligns with the triangle's geometric elements.

In essence, the method of using perpendicular bisectors offers a geometrically intuitive approach to pinpointing the circumcenter of a triangle. It not only unveils the precise location of this pivotal point but also enriches our understanding of the symmetrical and equilibrium properties inherent in the geometric structure of a triangle. This method serves as a cornerstone for comprehending the geometric significance of the circumcenter and its broader implications in diverse mathematical and practical contexts.

Method 2: Using the Intersection of Angle Bisectors

Utilizing the intersection of angle bisectors is another compelling method for determining the circumcenter of a triangle. An angle bisector is a line that divides an angle into two equal angles, and the intersection of these bisectors holds the key to locating the circumcenter.

To employ this method, we begin by identifying the three angle bisectors of the triangle, each emanating from a vertex and dividing the opposite angle into two congruent angles. The intersection point of these angle bisectors is the circumcenter of the triangle. This approach capitalizes on the geometric property that the circumcenter is equidistant from the triangle's vertices, a principle that manifests through the intersection of the angle bisectors.

By leveraging the intersection of angle bisectors, we gain a profound understanding of the circumcenter's role as a point of balance within the triangle. The convergence of the angle bisectors at the circumcenter signifies a harmonious equilibrium, where the distances from the circumcenter to the triangle's vertices are equal. This spatial symmetry highlights the circumcenter's pivotal position in maintaining the geometric stability and balance of the triangle.

Furthermore, the method of using angle bisectors to locate the circumcenter offers a unique perspective on the concept of concurrency in geometry. The intersection of the angle bisectors represents a point of concurrency, where the circumcenter seamlessly aligns with the triangle's geometric elements. This concurrency not only defines the circumcenter's precise location but also underscores its significance as a central point of equilibrium within the triangle.

In essence, the method of using the intersection of angle bisectors provides a geometrically elegant approach to pinpointing the circumcenter of a triangle. It not only reveals the precise location of this pivotal point but also deepens our understanding of the symmetrical and equilibrium properties inherent in the geometric structure of a triangle. This method serves as a cornerstone for comprehending the geometric significance of the circumcenter and its broader implications in diverse mathematical and practical contexts.

Method 3: Using Coordinates of Vertices

Utilizing the coordinates of vertices is a powerful method for determining the circumcenter of a triangle. This approach leverages the principles of coordinate geometry to precisely pinpoint the circumcenter based on the coordinates of the triangle's vertices. By employing this method, we can seamlessly integrate geometric concepts with algebraic techniques to unveil the spatial relationships and symmetrical properties inherent in the triangle.

To initiate the process, we first identify the coordinates of the triangle's three vertices, denoted as A(x1, y1), B(x2, y2), and C(x3, y3). With these coordinates in hand, we proceed to calculate the midpoints of the triangle's sides. The midpoint of a line segment with endpoints (x1, y1) and (x2, y2) can be determined using the midpoint formula as follows:

Midpoint = ((x1 + x2)/2, (y1 + y2)/2)

By applying this formula to each pair of vertices, we obtain the midpoints of the three sides of the triangle. These midpoints serve as crucial elements in the process of locating the circumcenter.

Next, we calculate the slopes of the lines containing the sides of the triangle. The slope of a line passing through points (x1, y1) and (x2, y2) can be computed using the slope formula:

Slope = (y2 – y1) / (x2 – x1)

With the slopes in hand, we then determine the perpendicular bisectors of the sides. The perpendicular bisector of a line segment with midpoint (x, y) and slope m can be expressed in the point-slope form of a line equation as:

y – y = -1/m(x – x)

By calculating the equations of the perpendicular bisectors for at least two sides of the triangle, we can then solve for their point of intersection. This point represents the circumcenter of the triangle, as it harmoniously aligns with the triangle's vertices based on their coordinates.

The method of using coordinates of vertices to locate the circumcenter offers a seamless integration of algebraic and geometric principles. It not only reveals the precise location of this pivotal point but also deepens our understanding of the symmetrical and equilibrium properties inherent in the geometric structure of a triangle. This method serves as a cornerstone for comprehending the geometric significance of the circumcenter and its broader implications in diverse mathematical and practical contexts.

Conclusion

In conclusion, the journey to unravel the mystery of the circumcenter of a triangle has provided us with profound insights into the geometric significance of this pivotal point. Through the exploration of multiple methods for determining the circumcenter, including using perpendicular bisectors, the intersection of angle bisectors, and the coordinates of vertices, we have gained a comprehensive understanding of the circumcenter's role as a central point of balance and equilibrium within a triangle.

The methods employed to locate the circumcenter have not only unveiled its precise geometric coordinates but have also shed light on the symmetrical and equilibrium properties inherent in the geometric structure of a triangle. The use of perpendicular bisectors has allowed us to appreciate the spatial relationships and concurrency within the triangle, emphasizing the circumcenter's role as a point of harmonious alignment. Similarly, the intersection of angle bisectors has provided a unique perspective on the circumcenter's significance as a central point of equilibrium, where the convergence of bisectors signifies a balanced spatial relationship with the triangle's vertices.

Furthermore, the integration of algebraic techniques with geometric principles in the method of using coordinates of vertices has enriched our understanding of the circumcenter's precise location based on the triangle's spatial coordinates. This approach has highlighted the seamless interplay between algebraic calculations and geometric concepts, underscoring the circumcenter's role as a point of spatial balance and symmetry within the triangle.

The significance of the circumcenter extends beyond its geometric properties, permeating into diverse fields such as engineering, architecture, and computational geometry. Its influence on the stability and equilibrium of structures, as well as its utilization in mathematical models and algorithms, underscores its broader implications in practical and theoretical contexts.

As we conclude this exploration, we recognize the circumcenter as a point of geometric harmony, where the intricate interplay between the triangle's elements converges to form a central point of equilibrium. The diverse methods employed to determine its location have not only enriched our understanding of the circumcenter's geometric significance but have also provided a gateway to exploring its broader implications in the realm of geometry and beyond. Thus, the circumcenter stands as a testament to the profound spatial relationships and symmetrical properties inherent in the geometric fabric of a triangle, embodying the delicate balance and harmony within this fundamental geometric construct.