Home>Mathematics>Unveiling The Mysterious Sequence: 4x^2 – 5x – 12 = 0
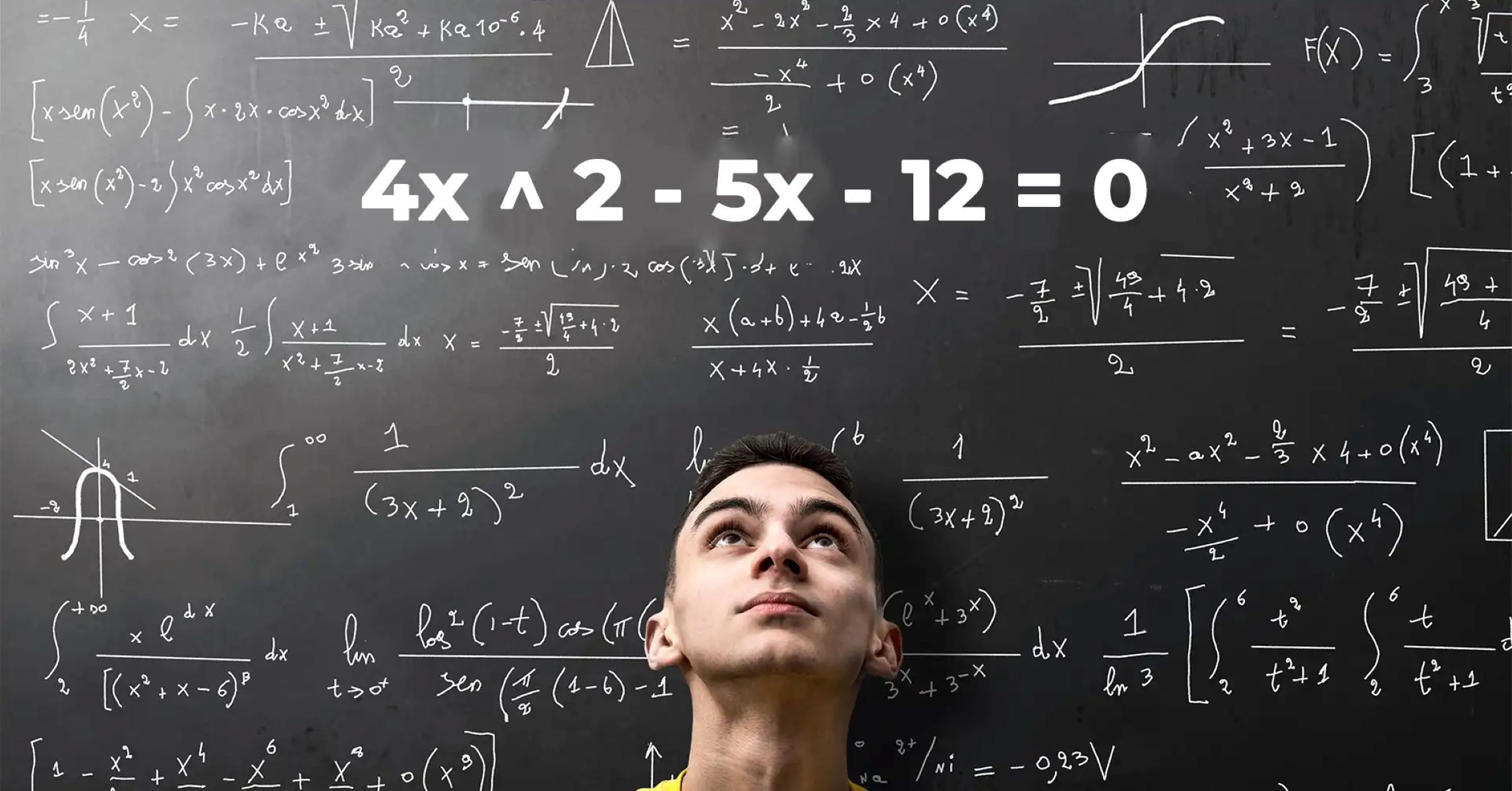
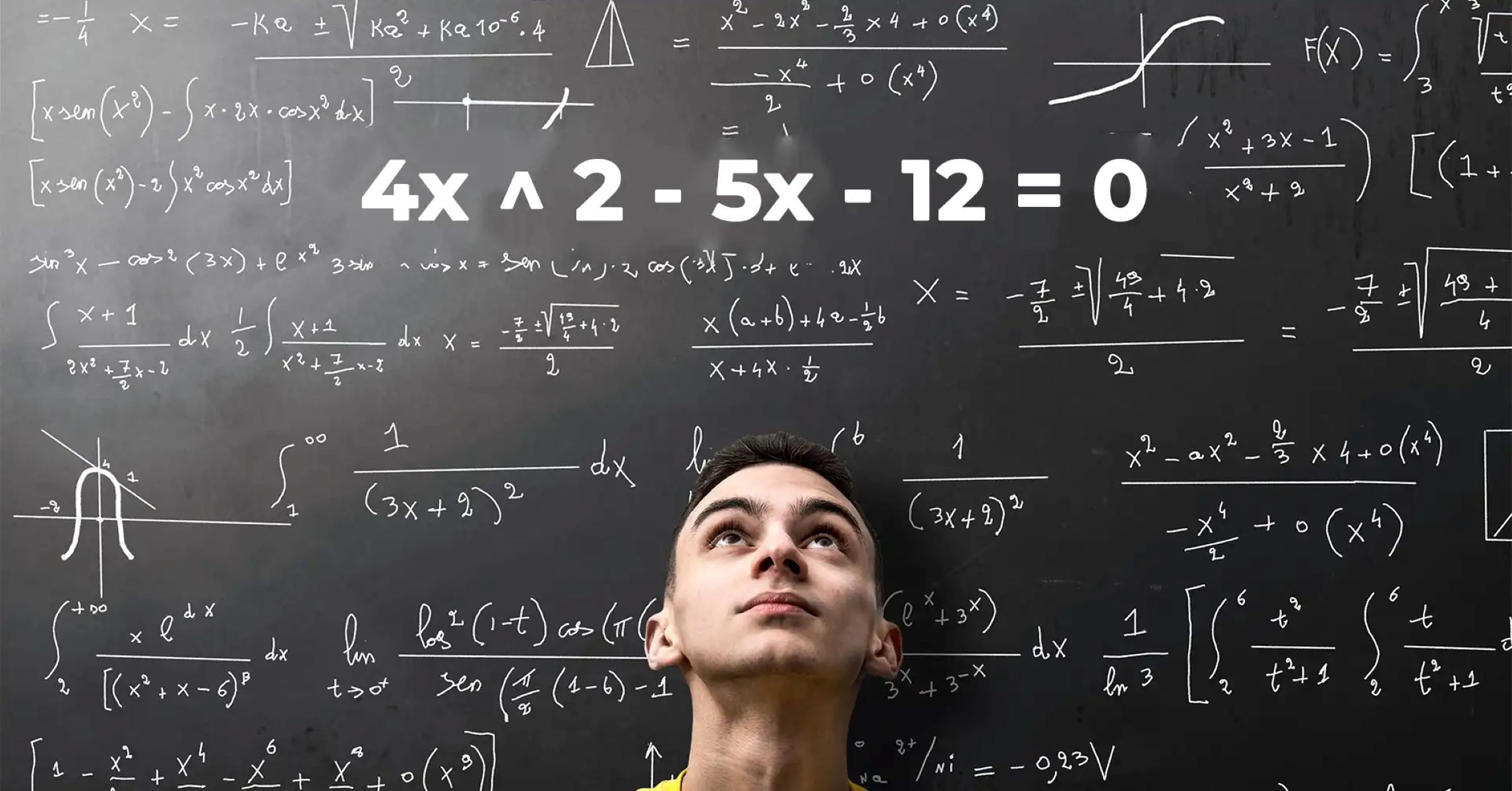
Mathematics
Unveiling The Mysterious Sequence: 4x^2 – 5x – 12 = 0
Published: January 13, 2024
Uncover the secrets of the enigmatic sequence 4x^2 - 5x - 12 = 0 in this intriguing exploration of mathematics. Discover the solutions and unravel the mysteries.
(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)
Table of Contents
Introduction
The enigmatic world of mathematics often presents us with intriguing puzzles and challenges, inviting us to delve into its depths and unravel the mysteries concealed within. One such enigma is the quadratic equation, a fundamental concept that has captivated the minds of mathematicians and students alike for centuries. At first glance, the quadratic equation may appear daunting, with its complex symbols and perplexing structure. However, beneath its seemingly impenetrable facade lies a captivating sequence that holds the key to unlocking a myriad of mathematical solutions.
The quadratic equation is a quintessential element of algebra, embodying the elegance and complexity inherent in mathematical expressions. Its standard form, ax^2 + bx + c = 0, where a, b, and c are constants, embodies a symphony of variables and coefficients that intertwine to form a distinctive pattern. This sequence, with its roots deeply embedded in the realm of parabolas and vertex points, beckons the inquisitive mind to embark on a journey of exploration and discovery.
As we embark on this mathematical odyssey, we will unravel the intricacies of the quadratic equation, peeling back its layers to reveal the essence of its structure and significance. Through this exploration, we will gain a deeper understanding of the methods employed to solve this enigmatic equation, shedding light on its profound implications in various mathematical and real-world contexts.
Join me as we embark on a captivating expedition into the realm of the quadratic equation, where the allure of mathematical patterns and the thrill of problem-solving converge to ignite the flames of curiosity and intellectual discovery. Through this journey, we will demystify the enigmatic sequence of 4x^2 – 5x – 12 = 0, unraveling its secrets and uncovering the profound beauty concealed within its mathematical essence.
Understanding the Quadratic Equation
The quadratic equation represents a fundamental cornerstone of algebra, encapsulating the elegance and complexity inherent in mathematical expressions. At its core, the quadratic equation is a second-degree polynomial equation, commonly expressed in the standard form ax^2 + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'x' represents the variable. This distinctive form embodies a symphony of variables and coefficients, defining a unique sequence that underpins a multitude of mathematical phenomena.
The graphical representation of a quadratic equation manifests as a parabola, a symmetrical curve with far-reaching implications in fields such as physics, engineering, and economics. The parabolic shape of the graph reflects the intricate interplay between the coefficients and variables within the quadratic equation, offering profound insights into the behavior of real-world phenomena.
In essence, the quadratic equation serves as a powerful tool for modeling a diverse array of natural and artificial systems, enabling mathematicians and scientists to analyze and predict complex relationships with precision and clarity. Its ubiquity in mathematical discourse underscores its significance as a foundational concept, permeating various branches of mathematics and serving as a linchpin for advanced mathematical theories and applications.
Moreover, the quadratic equation embodies a rich tapestry of mathematical properties and principles, offering a gateway to deeper comprehension of fundamental mathematical concepts. Through the exploration of the quadratic equation, students and enthusiasts alike gain invaluable insights into topics such as factorization, roots and solutions, vertex form, and the discriminant, fostering a holistic understanding of algebraic structures and their implications.
As we unravel the intricacies of the quadratic equation, we pave the way for a deeper appreciation of its role in shaping mathematical discourse and problem-solving strategies. By grasping the essence of this enigmatic sequence, we equip ourselves with a powerful lens through which to perceive and interpret the mathematical patterns that permeate our world, empowering us to engage with complex phenomena and derive meaningful insights from their mathematical underpinnings.
Solving the Quadratic Equation
Solving the quadratic equation is a captivating endeavor that unveils a spectrum of techniques and methodologies, each offering a unique vantage point from which to unravel the enigmatic sequence of 4x^2 – 5x – 12 = 0. At its essence, the process of solving a quadratic equation entails determining the values of the variable 'x' that satisfy the equation, thereby identifying the points at which the parabolic graph intersects the x-axis. This pursuit of solutions holds profound implications, transcending the realm of pure mathematics to permeate diverse fields such as physics, engineering, and economics.
One of the fundamental methods for solving a quadratic equation involves factoring, a technique that involves expressing the equation as a product of linear factors. By factoring the quadratic expression into two binomial factors, we can discern the values of 'x' that satisfy the equation, shedding light on the intricate relationship between the coefficients and variables within the sequence. This method not only provides a direct route to identifying the solutions of the equation but also offers valuable insights into the fundamental properties of quadratic expressions, fostering a deeper understanding of algebraic structures and their implications.
In instances where factoring proves to be elusive, the quadratic formula emerges as a powerful tool for unraveling the solutions of the equation. The quadratic formula, expressed as x = (-b ± √(b^2 – 4ac)) / (2a), encapsulates a symphony of mathematical operations that yield the values of 'x' corresponding to the solutions of the quadratic equation. This elegant formula serves as a testament to the ingenuity and sophistication of mathematical reasoning, providing a systematic and reliable method for addressing the enigmatic sequence of 4x^2 – 5x – 12 = 0.
Furthermore, the process of solving the quadratic equation transcends the realm of abstract mathematical manipulation, offering a gateway to intuitive problem-solving strategies and critical thinking skills. By engaging with the intricate process of unraveling the solutions of the quadratic equation, students and enthusiasts alike cultivate a profound appreciation for the beauty and elegance inherent in mathematical reasoning, equipping themselves with a versatile toolkit for addressing complex real-world problems with clarity and precision.
As we navigate the terrain of solving the quadratic equation, we embark on a journey of intellectual discovery, unearthing a treasure trove of mathematical techniques and insights that enrich our understanding of algebraic structures and their implications. Through this exploration, we not only demystify the enigmatic sequence of 4x^2 – 5x – 12 = 0 but also cultivate a deeper appreciation for the profound beauty concealed within its mathematical essence.
Factoring the Quadratic Equation
Factoring the quadratic equation is a fundamental method that unveils the intricate relationship between the coefficients and variables within the sequence, offering a compelling avenue to unravel the enigmatic sequence of 4x^2 – 5x – 12 = 0. This method, rooted in the principles of algebraic manipulation, embodies a symphony of mathematical operations that culminate in the expression of the quadratic equation as a product of linear factors. Through this process, we gain invaluable insights into the fundamental properties of quadratic expressions and their implications, fostering a deeper understanding of algebraic structures and their significance in mathematical discourse.
At the heart of factoring the quadratic equation lies the pursuit of expressing the quadratic expression as a product of two linear factors, thereby unveiling the values of 'x' that satisfy the equation. This endeavor encompasses a meticulous exploration of the coefficients 'a', 'b', and 'c' within the quadratic expression ax^2 + bx + c, as we seek to discern the factors that yield the original quadratic expression when multiplied together. By unraveling this intricate relationship, we illuminate the profound interplay between the variables and coefficients, paving the way for a deeper comprehension of the underlying algebraic structure.
The process of factoring the quadratic equation often involves leveraging the principles of factorization, a fundamental concept in algebraic reasoning. Through meticulous manipulation and analysis, we endeavor to express the quadratic expression as a product of two binomial factors, unveiling the roots or solutions of the equation. This method not only provides a direct route to identifying the solutions of the equation but also offers valuable insights into the fundamental properties of quadratic expressions, empowering us to engage with the underlying mathematical structure with clarity and precision.
Moreover, the process of factoring the quadratic equation transcends the realm of abstract mathematical manipulation, offering a gateway to intuitive problem-solving strategies and critical thinking skills. By engaging with the intricate process of unraveling the solutions of the quadratic equation through factorization, students and enthusiasts alike cultivate a profound appreciation for the beauty and elegance inherent in mathematical reasoning, equipping themselves with a versatile toolkit for addressing complex real-world problems with confidence and acumen.
As we navigate the terrain of factoring the quadratic equation, we embark on a journey of intellectual discovery, unearthing a treasure trove of mathematical techniques and insights that enrich our understanding of algebraic structures and their implications. Through this exploration, we not only demystify the enigmatic sequence of 4x^2 – 5x – 12 = 0 but also cultivate a deeper appreciation for the profound beauty concealed within its mathematical essence.
Using the Quadratic Formula
The quadratic formula stands as a venerable beacon of mathematical ingenuity, offering a systematic and reliable method for unraveling the solutions of a quadratic equation. Expressed as x = (-b ± √(b^2 – 4ac)) / (2a), this elegant formula encapsulates a symphony of mathematical operations that yield the values of 'x' corresponding to the solutions of the quadratic equation. By harnessing the power of the quadratic formula, we embark on a captivating journey that unveils the profound beauty concealed within the enigmatic sequence of 4x^2 – 5x – 12 = 0.
At the core of the quadratic formula lies a meticulous interplay between the coefficients 'a', 'b', and 'c' within the quadratic expression ax^2 + bx + c, culminating in the revelation of the solutions that underpin the equation. The discriminant, b^2 – 4ac, serves as a pivotal determinant of the nature of the solutions, offering insights into the behavior of the parabolic graph and the points at which it intersects the x-axis. Through the discernment of the discriminant's value, we gain a nuanced understanding of the nature of the solutions, paving the way for a comprehensive exploration of the quadratic equation's implications.
Moreover, the quadratic formula serves as a testament to the elegance and sophistication of mathematical reasoning, providing a versatile toolkit for addressing a diverse array of quadratic equations with precision and clarity. Its systematic structure and reliance on fundamental mathematical operations render it an indispensable asset in the pursuit of unraveling the enigmatic sequence of 4x^2 – 5x – 12 = 0, empowering mathematicians and students alike to engage with complex algebraic structures with confidence and acumen.
As we immerse ourselves in the process of utilizing the quadratic formula, we embark on a journey of intellectual discovery, unearthing a treasure trove of mathematical techniques and insights that enrich our understanding of algebraic structures and their implications. Through this exploration, we not only demystify the enigmatic sequence of 4x^2 – 5x – 12 = 0 but also cultivate a deeper appreciation for the profound beauty concealed within its mathematical essence.
The quadratic formula stands as a timeless testament to the enduring allure and significance of mathematical reasoning, inviting us to engage with its symphony of operations and unveil the solutions that lie at the heart of the enigmatic sequence. In doing so, we equip ourselves with a powerful lens through which to perceive and interpret the mathematical patterns that permeate our world, empowering us to engage with complex phenomena and derive meaningful insights from their mathematical underpinnings.
Conclusion
In the realm of mathematics, the enigmatic sequence of 4x^2 – 5x – 12 = 0 serves as a captivating emblem of the profound beauty and complexity inherent in algebraic structures. Through our exploration of the quadratic equation and its various methods of solution, we have embarked on a captivating journey of intellectual discovery, unearthing a treasure trove of mathematical techniques and insights that enrich our understanding of algebraic structures and their implications.
As we conclude our expedition into the realm of the quadratic equation, we emerge with a profound appreciation for the elegance and significance of mathematical reasoning. The quadratic equation, with its parabolic graph and symmetrical curves, offers a gateway to intuitive problem-solving strategies and critical thinking skills. By engaging with the intricate process of unraveling the solutions of the quadratic equation, we have cultivated a deep appreciation for the beauty and elegance inherent in mathematical reasoning, equipping ourselves with a versatile toolkit for addressing complex real-world problems with confidence and acumen.
Moreover, the journey of solving the quadratic equation has transcended mere mathematical manipulation, offering profound insights into the nature of parabolas, vertex points, and the behavior of real-world phenomena. The quadratic equation, in its standard form ax^2 + bx + c = 0, embodies a symphony of variables and coefficients that intertwine to form a distinctive pattern, reflecting the intricate interplay between the mathematical expressions and the real-world applications they represent.
Through our exploration, we have demystified the enigmatic sequence of 4x^2 – 5x – 12 = 0, unraveling its secrets and uncovering the profound beauty concealed within its mathematical essence. This journey has not only enriched our understanding of algebraic structures but has also empowered us to engage with complex phenomena and derive meaningful insights from their mathematical underpinnings.
In essence, the quadratic equation stands as a timeless testament to the enduring allure and significance of mathematical reasoning, inviting us to engage with its symphony of operations and unveil the solutions that lie at the heart of the enigmatic sequence. As we conclude this exploration, we carry with us a deepened understanding of the elegance and complexity inherent in the quadratic equation, embracing its role as a foundational concept that permeates various branches of mathematics and serves as a linchpin for advanced mathematical theories and applications.