The Ultimate Guide To Finding The Perfect Rectangle In A Circle!

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)

Introduction

Welcome to the ultimate guide to finding the perfect rectangle in a circle! In the world of mathematics, the relationship between rectangles and circles is a fascinating and intricate subject that has captivated the minds of scholars and enthusiasts for centuries. This guide will delve into the depths of this relationship, exploring the concepts of maximum area and maximum perimeter rectangles inside a circle, and providing practical applications and examples to illustrate their significance.

The exploration of rectangles within circles is not merely an abstract exercise in geometry; it has real-world implications and applications that extend far beyond the confines of a mathematical realm. By understanding the fundamental principles that govern the placement of rectangles within circles, we can unlock valuable insights that have practical implications in fields such as architecture, engineering, design, and optimization.

Throughout this guide, we will embark on a journey to uncover the secrets of maximizing the area and perimeter of a rectangle inscribed within a circle. By unraveling these concepts, we can gain a deeper appreciation for the elegant interplay between geometric shapes and the underlying principles that govern their interactions.

So, whether you are a student seeking to expand your knowledge of geometry, an aspiring architect aiming to optimize spatial design, or a curious mind intrigued by the beauty of mathematical relationships, this guide is designed to equip you with the knowledge and understanding to navigate the intricate landscape of rectangles within circles.

Join me as we embark on a mathematical odyssey, exploring the symbiotic relationship between rectangles and circles, and unveiling the practical significance of these concepts in the world around us. Let's dive into the realm of geometric wonders and unlock the secrets of finding the perfect rectangle in a circle!

Understanding the Relationship Between Rectangles and Circles

The relationship between rectangles and circles is a captivating exploration of geometric interplay that unveils a rich tapestry of mathematical connections. At the heart of this relationship lies the concept of inscribing a rectangle within a circle, a fundamental geometric puzzle that has intrigued scholars and mathematicians throughout history.

When a rectangle is inscribed within a circle, it becomes intricately bound by the circular boundary, creating a symbiotic relationship that transcends mere spatial arrangement. The dimensions of the rectangle, including its length and width, are inherently constrained by the circumference of the enclosing circle, giving rise to a delicate balance between the two geometric entities.

One of the key insights that emerges from this relationship is the realization that the dimensions of the inscribed rectangle directly influence the properties of the enclosing circle. As the dimensions of the rectangle vary, the circle adapts to accommodate the changing spatial dynamics, resulting in a dynamic interplay of geometric proportions.

Moreover, the relationship between rectangles and circles extends beyond mere spatial arrangement; it delves into the realm of optimization and efficiency. By inscribing a rectangle within a circle, we are presented with the opportunity to maximize either the area or the perimeter of the rectangle while operating within the confines of the circular boundary. This fundamental optimization challenge forms the crux of the relationship between rectangles and circles, offering a tantalizing glimpse into the intricacies of geometric efficiency.

As we unravel the intricate relationship between rectangles and circles, we gain a deeper appreciation for the harmonious coexistence of these geometric entities. The interplay between the angular precision of rectangles and the graceful curvature of circles exemplifies the seamless fusion of disparate geometric elements, giving rise to a symphony of mathematical elegance.

In essence, the relationship between rectangles and circles transcends the confines of mere spatial arrangement, evolving into a profound exploration of geometric harmony, optimization, and interdependence. By understanding and embracing this relationship, we can unlock a world of geometric insights that have far-reaching implications across various fields, from architecture and engineering to design and optimization.

The journey to comprehend the intricate relationship between rectangles and circles is a testament to the enduring allure of geometric exploration, offering a gateway to a realm where mathematical elegance converges with practical significance. It is within this captivating landscape that we begin to unravel the secrets of finding the perfect rectangle in a circle, setting the stage for a deeper exploration of geometric wonders.

This is just the beginning of our journey into the fascinating world of rectangles and circles, where the interplay of geometric shapes unveils a myriad of insights and possibilities. As we delve deeper into this captivating realm, we will uncover the principles that govern the placement of rectangles within circles, and illuminate the practical applications that stem from this timeless relationship. Join me as we embark on this geometric odyssey, unraveling the mysteries that lie at the intersection of rectangles and circles.

Finding the Maximum Area Rectangle Inside a Circle

When it comes to finding the maximum area rectangle inside a circle, we are confronted with a captivating optimization challenge that demands a delicate balance between geometric dimensions and spatial efficiency. The quest to maximize the area of a rectangle inscribed within a circle requires a nuanced understanding of the interplay between the circular boundary and the inherent properties of the rectangle.

To embark on this exploration, we begin by acknowledging the fundamental principle that governs the relationship between the rectangle and the circle. As the dimensions of the rectangle vary, the area enclosed within its boundaries undergoes a corresponding transformation, directly impacting the overall spatial efficiency. However, the circular boundary imposes constraints on the dimensions of the rectangle, compelling us to navigate the intricate landscape of geometric optimization.

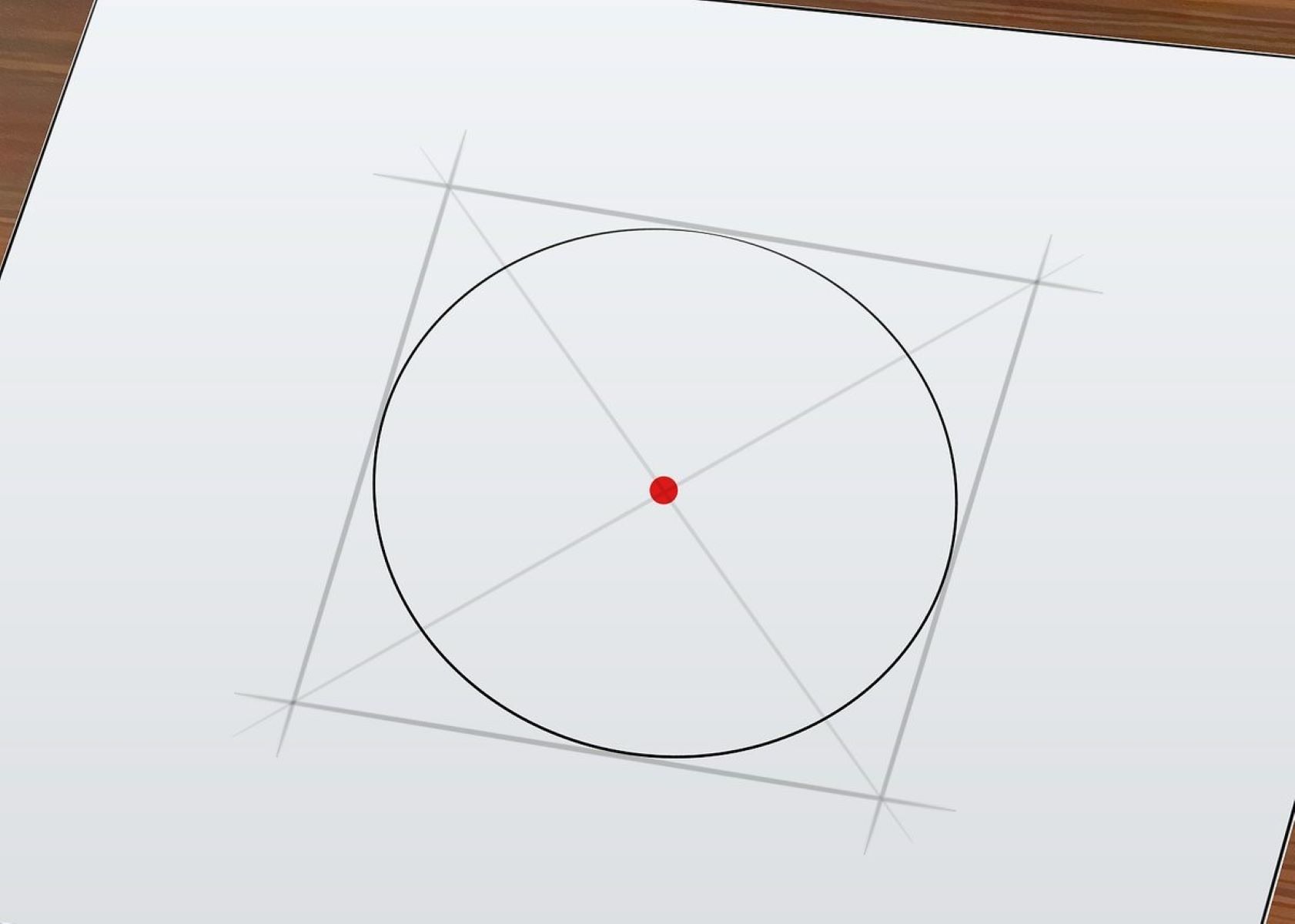
In the pursuit of maximizing the area of the inscribed rectangle, we encounter a pivotal insight that guides our exploration: the square. It is within the realm of squares that we unearth the key to unlocking the maximum area within the circular confines. By inscribing a square within the circle, we achieve the optimal utilization of space, as the square's equal sides align with the circular boundary, maximizing the enclosed area.

The significance of the square as the optimal area-maximizing rectangle within a circle lies in its symmetrical properties. With all sides equal, the square seamlessly integrates with the circular boundary, creating a spatial harmony that culminates in the maximum area configuration. This elegant interplay between the square and the circle exemplifies the inherent balance and efficiency that underpin geometric optimization.

As we delve deeper into the realm of maximizing the area of a rectangle inside a circle, the square serves as a guiding beacon, illuminating the path toward spatial efficiency and geometric elegance. By embracing the principles that govern the relationship between the square and the circle, we gain a profound appreciation for the delicate interplay of geometric elements and the enduring quest for optimization.

In essence, the pursuit of finding the maximum area rectangle inside a circle is a testament to the enduring allure of geometric optimization, where the balance between spatial dimensions and efficiency converges to unlock a world of geometric possibilities. Through the exploration of the square's role as the optimal area-maximizing rectangle, we unravel the timeless principles that govern the interplay between rectangles and circles, paving the way for a deeper understanding of geometric harmony and spatial efficiency.

Finding the Maximum Perimeter Rectangle Inside a Circle

In the quest to find the maximum perimeter rectangle inside a circle, we embark on a captivating exploration of geometric optimization and spatial efficiency. Unlike the pursuit of maximizing the area, which led us to the elegant symmetrical properties of the square, the quest to maximize the perimeter of a rectangle within a circle presents a unique set of challenges and insights.

As we delve into this exploration, we encounter a fundamental principle that guides our journey: the concept of a golden rectangle. The golden rectangle, renowned for its aesthetically pleasing proportions and inherent geometric harmony, emerges as a pivotal archetype in our quest to maximize the perimeter within the circular confines. With its distinctive aspect ratio, the golden rectangle encapsulates the essence of spatial efficiency and geometric elegance, offering valuable insights into the optimization of perimeter within a circular boundary.

The allure of the golden rectangle lies in its unique properties, characterized by a specific ratio between its length and width, known as the golden ratio. This ratio, approximately equal to 1.618, embodies a harmonious balance that transcends mere geometric dimensions, reflecting a timeless principle of aesthetic appeal and spatial efficiency. When inscribed within a circle, the golden rectangle harnesses its inherent proportions to maximize the perimeter, seamlessly aligning with the circular boundary to optimize the spatial enclosure.

Moreover, the golden rectangle's capacity to maximize the perimeter within a circle is a testament to the enduring quest for geometric efficiency and balance. By embracing the principles that govern the relationship between the golden rectangle and the circular boundary, we unravel a world of geometric elegance and optimization, where the interplay of proportions and spatial constraints converges to unlock a realm of possibilities.

In essence, the pursuit of finding the maximum perimeter rectangle inside a circle transcends the confines of mere spatial dimensions, evolving into a profound exploration of geometric harmony and efficiency. Through the captivating lens of the golden rectangle, we gain a deeper appreciation for the delicate balance between perimeter optimization and spatial constraints, illuminating the timeless principles that govern the interplay between rectangles and circles.

As we navigate the intricate landscape of maximizing the perimeter within a circular boundary, the golden rectangle stands as a testament to the enduring allure of geometric optimization, offering a gateway to a realm where spatial proportions and efficiency converge to unveil a world of geometric wonders. This exploration serves as a testament to the enduring quest for geometric elegance and optimization, where the pursuit of maximizing the perimeter within a circle transcends the confines of mere spatial dimensions, evolving into a profound exploration of geometric harmony and efficiency. Through the captivating lens of the golden rectangle, we gain a deeper appreciation for the delicate balance between perimeter optimization and spatial constraints, illuminating the timeless principles that govern the interplay between rectangles and circles.

Practical Applications and Examples

The principles governing the relationship between rectangles and circles extend far beyond the realm of theoretical geometry, finding practical applications in diverse fields such as architecture, engineering, design, and optimization. By delving into the practical applications and examples of inscribing rectangles within circles, we uncover a myriad of real-world scenarios where these geometric concepts play a pivotal role.

Architecture and Spatial Design

In the realm of architecture, the optimization of spatial layouts and the efficient utilization of space are paramount considerations. The concept of inscribing rectangles within circles offers architects and designers valuable insights into maximizing usable space while adhering to spatial constraints. By strategically placing rectangular structures within circular boundaries, architects can optimize spatial efficiency, creating harmonious and visually appealing designs that seamlessly integrate geometric elements.

Engineering and Structural Optimization

In the field of engineering, the principles of maximizing area and perimeter within defined boundaries are crucial for structural optimization. The insights gained from inscribing rectangles within circles can be applied to the design of bridges, buildings, and infrastructure, where the efficient allocation of resources and the optimization of spatial dimensions are essential. By leveraging the geometric principles of inscribed rectangles, engineers can enhance the structural integrity and efficiency of various constructions, leading to cost-effective and aesthetically pleasing solutions.

Industrial Design and Product Optimization

In the realm of industrial design, the placement of components within circular enclosures plays a pivotal role in product optimization. By applying the principles of inscribing rectangles within circles, industrial designers can maximize the utility of available space, leading to the efficient placement of components within circular housings. This approach not only enhances the functionality of products but also contributes to streamlined manufacturing processes and cost-effective production.

Urban Planning and Spatial Organization

In urban planning and spatial organization, the efficient allocation of public spaces and the optimization of urban layouts are fundamental considerations. The concept of inscribing rectangles within circles offers valuable insights into optimizing public spaces, parks, and recreational areas within circular boundaries. By strategically placing rectangular features within circular environments, urban planners can create visually striking and functional spaces that harmonize with the natural landscape, contributing to the overall aesthetic appeal and usability of urban environments.

Environmental Design and Resource Optimization

In the domain of environmental design, the efficient allocation of resources and the optimization of spatial configurations are essential for sustainable development. By leveraging the principles of inscribing rectangles within circles, environmental designers can maximize the utilization of available resources, leading to the creation of sustainable and environmentally conscious designs. Whether it involves the layout of solar panels within circular arrays or the optimization of agricultural plots within circular boundaries, the application of geometric principles offers valuable insights into resource optimization and sustainable design practices.

In summary, the practical applications of inscribing rectangles within circles extend across a diverse spectrum of fields, offering valuable insights into spatial optimization, structural efficiency, product design, urban planning, and sustainable development. By embracing the geometric principles that govern this relationship, professionals across various disciplines can unlock a world of possibilities, leading to innovative solutions and optimized designs that harmonize with the natural environment while maximizing spatial efficiency.

Conclusion

In conclusion, the exploration of rectangles within circles transcends the confines of theoretical geometry, extending into a realm where practical applications and real-world significance converge with the timeless principles of geometric harmony and optimization. Throughout this journey, we have delved into the intricate relationship between rectangles and circles, unraveling the secrets of finding the perfect rectangle within the circular confines. From the pursuit of maximizing area to the quest for optimizing perimeter, we have navigated a captivating landscape where geometric elegance converges with practical implications.

The pursuit of finding the maximum area rectangle inside a circle led us to the symmetrical properties of the square, illuminating the path toward spatial efficiency and geometric elegance. By inscribing a square within the circular boundary, we achieved the optimal utilization of space, showcasing the seamless integration of geometric elements and the enduring quest for optimization. The square emerged as a beacon of spatial efficiency, embodying the balance between geometric dimensions and the circular boundary, unveiling the timeless principles that govern the interplay between rectangles and circles.

Similarly, the exploration of maximizing the perimeter within a circular boundary unveiled the captivating allure of the golden rectangle, renowned for its aesthetically pleasing proportions and inherent geometric harmony. With its distinctive aspect ratio and the embodiment of the golden ratio, the golden rectangle encapsulated the essence of spatial efficiency and optimization, offering valuable insights into maximizing perimeter within the circular confines. Through the lens of the golden rectangle, we gained a deeper appreciation for the delicate balance between perimeter optimization and spatial constraints, illuminating the timeless principles that govern the interplay between rectangles and circles.

Moreover, the practical applications of inscribing rectangles within circles extend across diverse fields, from architecture and engineering to urban planning and environmental design. The principles of spatial optimization, structural efficiency, product design, and sustainable development are enriched by the timeless geometric insights gained from this exploration. By embracing the interplay of rectangles and circles, professionals across various disciplines can unlock a world of possibilities, leading to innovative solutions and optimized designs that harmonize with the natural environment while maximizing spatial efficiency.

In essence, the journey to find the perfect rectangle in a circle is a testament to the enduring allure of geometric exploration, offering a gateway to a realm where mathematical elegance converges with practical significance. By unraveling the timeless principles that govern the relationship between rectangles and circles, we have embarked on a captivating odyssey that illuminates the intricate interplay of geometric shapes and the enduring quest for optimization. As we conclude this exploration, we carry with us a deeper understanding of the delicate balance between spatial dimensions and efficiency, paving the way for a world of geometric wonders and practical applications that enrich our understanding of the world around us.