The Ultimate Triangle Secret: A Pythagorean Theorem For Every Shape!

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)

Introduction

Welcome to the fascinating world of the Pythagorean Theorem! This ancient mathematical principle, attributed to the Greek mathematician Pythagoras, has intrigued and inspired scholars, mathematicians, and problem-solvers for centuries. At its core, the Pythagorean Theorem offers a profound insight into the relationships between the sides of a right-angled triangle, making it a cornerstone of geometry and a fundamental tool in various real-world applications.

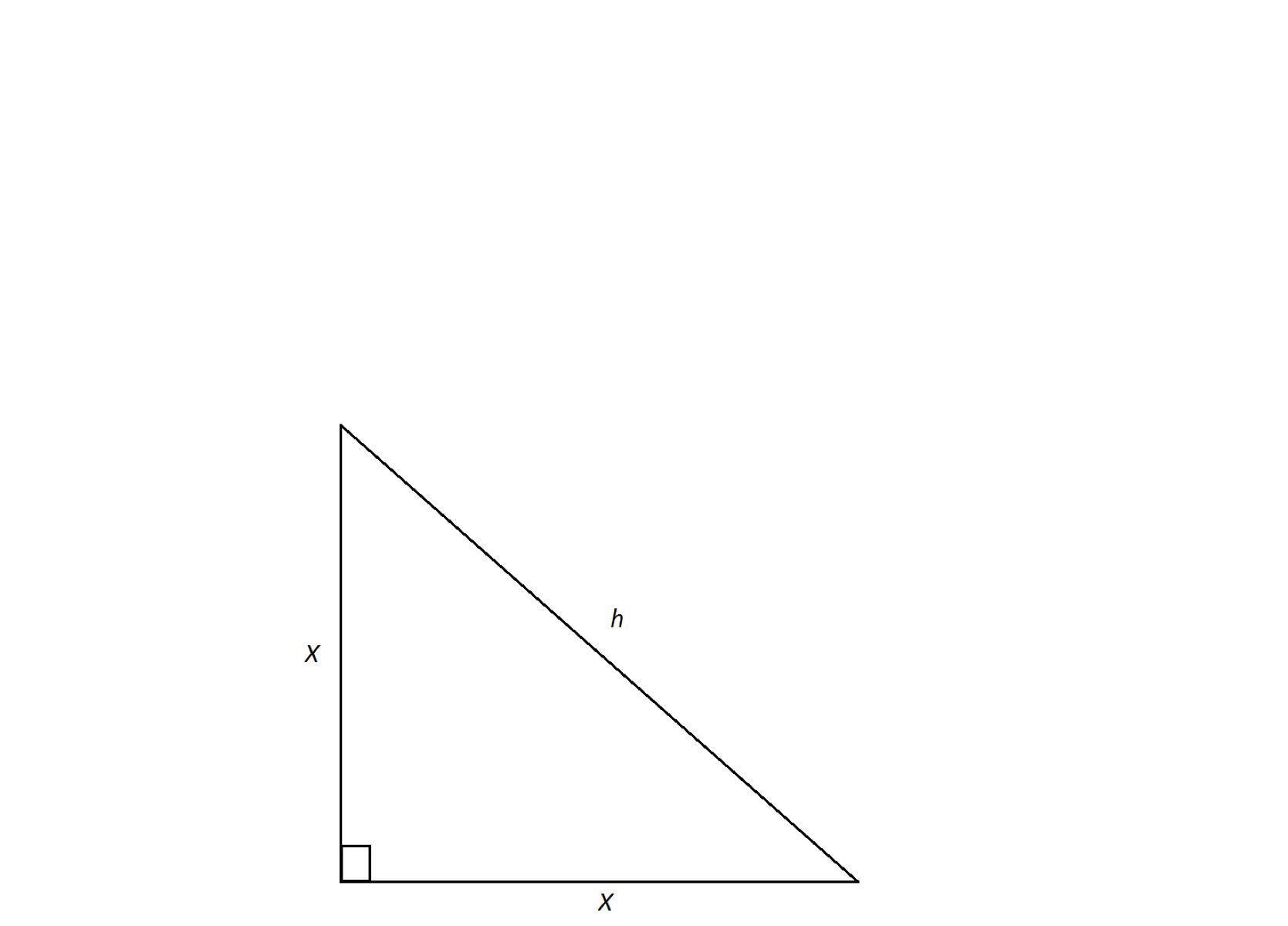
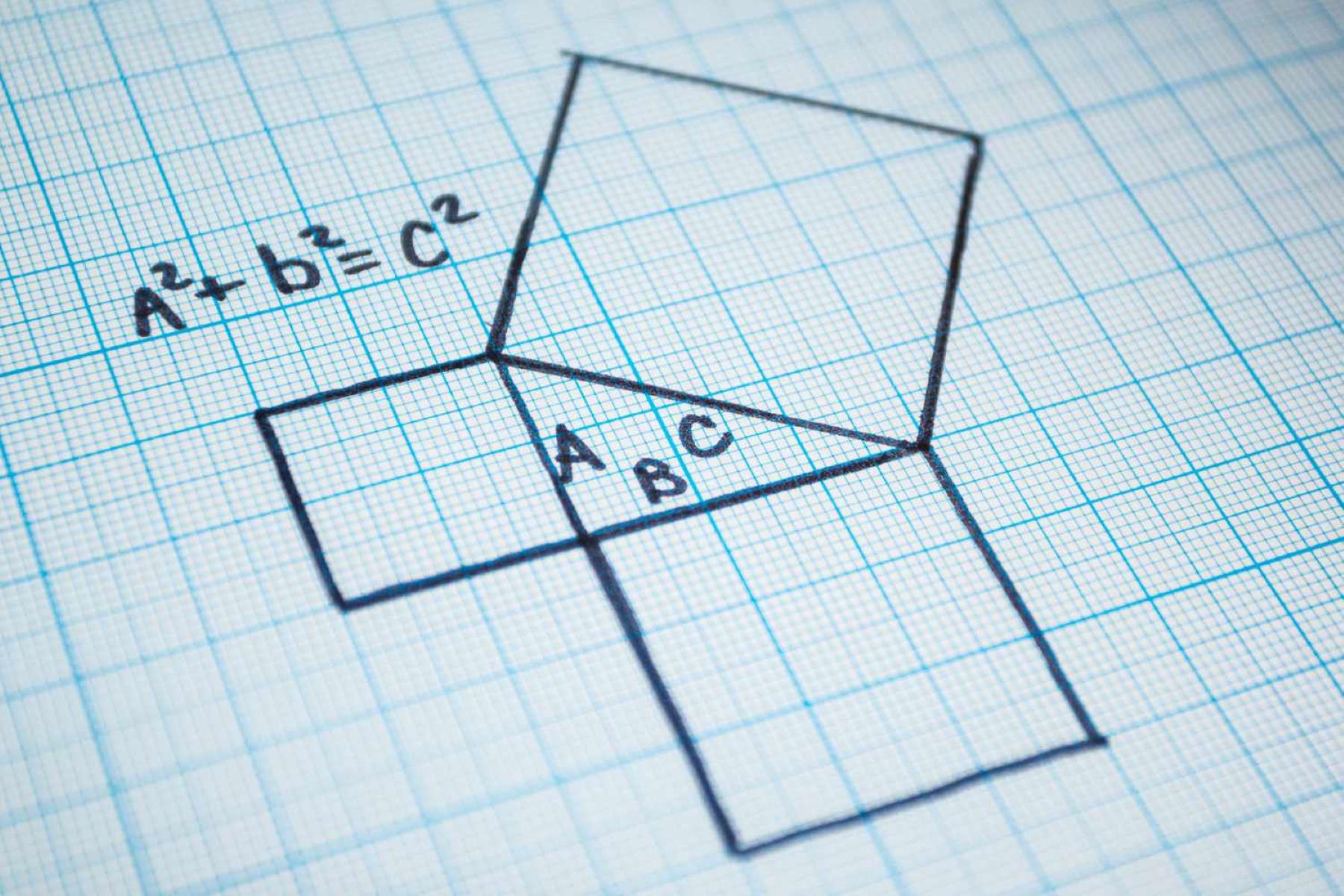
The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This elegant relationship is expressed as a simple algebraic equation: a^2 + b^2 = c^2, where 'a' and 'b' represent the lengths of the two shorter sides, and 'c' represents the length of the hypotenuse. This fundamental principle forms the basis for countless geometric calculations and practical problem-solving scenarios.

As we delve into the depths of the Pythagorean Theorem, we will uncover its timeless significance and explore its versatility beyond the realm of traditional right-angled triangles. By extending the principles of this theorem to various shapes and dimensions, we can unlock a treasure trove of mathematical insights and practical applications. Join us on this illuminating journey as we unravel the ultimate triangle secret and discover a Pythagorean Theorem for every shape!

Understanding the Pythagorean Theorem

The Pythagorean Theorem is a foundational concept in geometry that holds immense significance in both theoretical mathematics and real-world applications. At its essence, this theorem provides a profound relationship between the sides of a right-angled triangle, offering a precise and elegant means of calculating unknown dimensions and solving a myriad of problems.

In a right-angled triangle, the side opposite the right angle is known as the hypotenuse, while the other two sides are referred to as the legs. The Pythagorean Theorem asserts that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This relationship is succinctly expressed as a^2 + b^2 = c^2, where 'a' and 'b' represent the lengths of the legs, and 'c' represents the length of the hypotenuse.

This fundamental principle can be visualized as a powerful tool for determining unknown side lengths within a right-angled triangle. By applying the Pythagorean Theorem, mathematicians and problem-solvers can effortlessly calculate the length of a missing side when provided with the measurements of the other two sides. Moreover, this theorem serves as the cornerstone for various geometric calculations, such as determining distances, solving for unknown angles, and establishing the stability of structures in engineering and architecture.

The beauty of the Pythagorean Theorem lies in its universality and timelessness. Its applicability extends beyond the confines of traditional geometric shapes, permeating into diverse fields such as physics, astronomy, and navigation. This enduring relevance underscores the theorem's status as a fundamental building block of mathematical understanding and problem-solving prowess.

As we grasp the essence of the Pythagorean Theorem, we gain a deeper appreciation for its elegance and utility. This foundational principle not only enriches our understanding of geometry but also empowers us to unravel the mysteries of space, shape, and dimension. With this profound understanding, we are primed to embark on an exploration of the extended applications of the Pythagorean Theorem, where its timeless principles converge with the complexities of diverse shapes and dimensions, unlocking a world of mathematical marvels.

Extending the Pythagorean Theorem to Different Shapes

The Pythagorean Theorem, revered for its elegance and practicality in the realm of right-angled triangles, transcends its traditional boundaries to embrace a myriad of shapes and dimensions. As we venture into the realm of non-traditional geometries, the timeless principles of the Pythagorean Theorem unveil a world of possibilities, offering profound insights into the relationships between sides, angles, and dimensions.

One of the most remarkable extensions of the Pythagorean Theorem involves its application to three-dimensional shapes, particularly right-angled prisms and pyramids. In these complex geometries, the Pythagorean Theorem manifests as a powerful tool for calculating distances, determining spatial relationships, and unraveling the intricacies of three-dimensional space. By applying the principles of the theorem to the faces, edges, and diagonals of these polyhedral structures, mathematicians and engineers can navigate the complexities of spatial geometry with precision and clarity.

Furthermore, the Pythagorean Theorem extends its reach to encompass the realm of circles and spheres, offering profound insights into the relationships between radii, diameters, and circumferences. By leveraging the principles of the theorem, mathematicians and physicists can unravel the mysteries of circular and spherical geometries, deriving essential formulas for calculating areas, volumes, and critical dimensions. This extension of the theorem underscores its versatility and enduring relevance in diverse branches of mathematics and scientific inquiry.

Beyond traditional geometric shapes, the Pythagorean Theorem finds application in the realm of trigonometry, where it serves as the foundation for the sine, cosine, and tangent functions. These fundamental trigonometric relationships, derived from the principles of the Pythagorean Theorem, enable mathematicians, engineers, and scientists to navigate the complexities of angles, rotations, and oscillations, forming the bedrock of modern calculus, physics, and engineering disciplines.

As we witness the far-reaching implications of extending the Pythagorean Theorem to different shapes and dimensions, we gain a profound appreciation for its timeless significance and enduring relevance. This extension not only enriches our understanding of geometry and spatial relationships but also empowers us to unravel the complexities of three-dimensional space, circular geometries, and trigonometric functions with clarity and precision. In essence, the Pythagorean Theorem transcends its origins to embrace a world of mathematical marvels, offering profound insights into the fabric of our geometric universe.

Applications of the Extended Pythagorean Theorem

The extended applications of the Pythagorean Theorem encompass a diverse array of real-world scenarios, where its timeless principles converge with the complexities of various shapes and dimensions, unlocking a world of mathematical marvels.

In the realm of engineering and architecture, the extended Pythagorean Theorem plays a pivotal role in structural stability analysis. By applying the principles of the theorem to three-dimensional shapes and polyhedral structures, engineers can calculate diagonal distances within complex frameworks, ensuring the integrity and stability of architectural designs. This application is particularly relevant in the construction of trusses, frames, and support systems, where precise measurements and spatial relationships are critical to the safety and functionality of the built environment.

Furthermore, the extended Pythagorean Theorem finds profound applications in the field of navigation and geospatial analysis. By leveraging the principles of three-dimensional geometry and spherical trigonometry, navigators and cartographers can calculate distances, bearings, and angular relationships on the Earth's surface with remarkable precision. This application is essential for charting courses, determining positions, and navigating vast expanses of land and sea, underpinning the foundations of modern maritime and aerial navigation.

Moreover, the extended Pythagorean Theorem permeates into the realm of physics and astronomy, where it serves as a fundamental tool for calculating distances, trajectories, and spatial relationships in celestial bodies and planetary systems. By applying the principles of circular and spherical geometry, physicists and astronomers can unravel the mysteries of orbital mechanics, planetary motion, and celestial dynamics, shedding light on the fundamental principles that govern the cosmic dance of celestial bodies.

In the domain of technological innovation, the extended Pythagorean Theorem fuels advancements in computer graphics, virtual reality, and 3D modeling. By harnessing the principles of spatial geometry and three-dimensional trigonometry, software developers and graphic designers can create immersive virtual environments, simulate realistic physical interactions, and render complex visualizations with unparalleled accuracy and realism. This application underscores the theorem's relevance in shaping the technological landscape and driving innovation in the digital realm.

As we contemplate the myriad applications of the extended Pythagorean Theorem, we gain a profound appreciation for its enduring relevance and far-reaching impact across diverse fields. From engineering and navigation to physics and technology, the timeless principles of the Pythagorean Theorem continue to illuminate the path of human ingenuity, offering profound insights into the fabric of our geometric universe and empowering us to navigate the complexities of space, shape, and dimension with clarity and precision.

Conclusion

In the grand tapestry of mathematics, the Pythagorean Theorem stands as a timeless beacon of geometric insight and practical utility. From its humble origins in the realm of right-angled triangles, this fundamental principle extends its reach to embrace a myriad of shapes and dimensions, offering profound insights into the fabric of our geometric universe. As we navigate the complexities of space, shape, and dimension, the Pythagorean Theorem emerges as a steadfast companion, guiding us through the intricacies of spatial relationships, structural stability, celestial mechanics, and technological innovation.

The journey of exploration and discovery has illuminated the enduring relevance and far-reaching impact of the Pythagorean Theorem. Its elegant principles, encapsulated in the simple equation a^2 + b^2 = c^2, resonate across diverse fields, permeating into the realms of engineering, navigation, physics, and technology. In the domain of structural analysis, the theorem serves as a cornerstone for ensuring the stability and integrity of architectural designs, providing engineers with a powerful tool for calculating spatial relationships within complex frameworks. Moreover, in the realm of navigation, the theorem empowers navigators and cartographers to chart courses, determine positions, and navigate vast expanses of land and sea with precision and accuracy, underpinning the foundations of modern maritime and aerial navigation.

Furthermore, the Pythagorean Theorem finds profound applications in the exploration of celestial mechanics and planetary motion, offering physicists and astronomers a fundamental tool for unraveling the mysteries of orbital dynamics, planetary trajectories, and celestial interactions. Its extension into the realm of technology fuels advancements in computer graphics, virtual reality, and 3D modeling, shaping the digital landscape and driving innovation in the realms of visualization and simulation.

As we reflect on the enduring legacy of the Pythagorean Theorem, we are reminded of its profound impact on human ingenuity and problem-solving prowess. Its timeless principles continue to inspire and empower generations of mathematicians, engineers, scientists, and innovators, offering a glimpse into the harmonious interplay between mathematical elegance and practical utility. In essence, the Pythagorean Theorem transcends its origins to embrace a world of mathematical marvels, offering profound insights into the fabric of our geometric universe and empowering us to navigate the complexities of space, shape, and dimension with clarity and precision.