Home>Mathematics>The Mind-Blowing Secret To Finding The Derivative Of Xy!
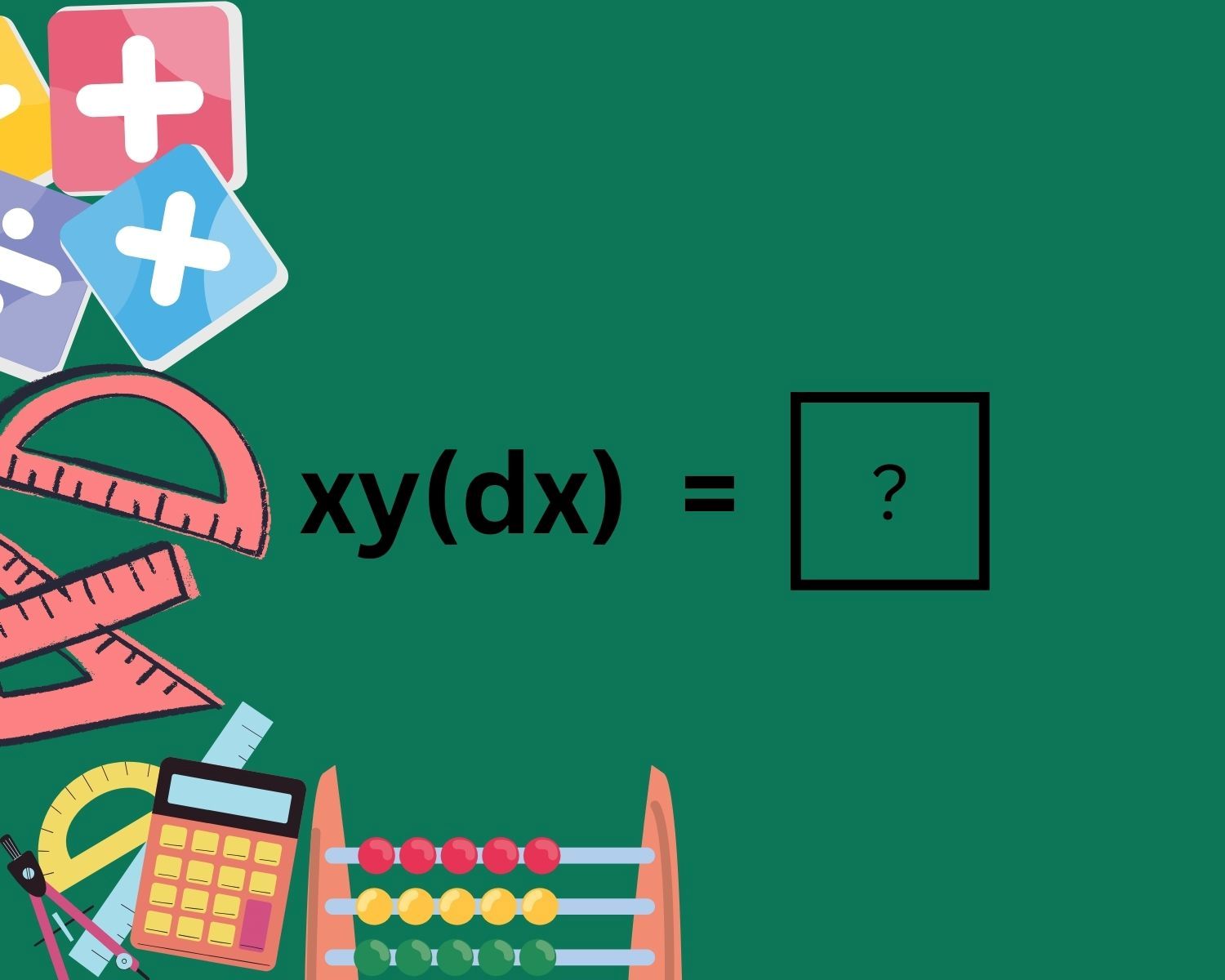
Mathematics
The Mind-Blowing Secret To Finding The Derivative Of Xy!
Published: January 7, 2024
Discover the mind-blowing secret to finding the derivative of xy! Dive into the world of mathematics and unlock the power of derivatives with this groundbreaking technique.
(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)
Table of Contents
Introduction
The world of mathematics is filled with captivating secrets and mind-bending concepts that continue to intrigue and challenge both students and experts alike. One such enigma lies in the realm of calculus, where the derivative of a function represents a fundamental concept with far-reaching applications. In this article, we will unravel the mind-blowing secret to finding the derivative of xy! Yes, you read that correctly – the derivative of xy factorial!
The notion of derivatives, first introduced by the legendary mathematician Isaac Newton, revolutionized the way we perceive and understand change. Whether it's the velocity of a moving object, the rate of growth of a population, or the slope of a curve, derivatives serve as the mathematical tool that unlocks the mysteries of transformation and variation. And when we venture into the realm of factorials, where numbers are multiplied consecutively from the given number down to 1, the intrigue deepens even further.
The derivative of xy factorial presents a fascinating challenge that beckons us to explore the depths of calculus and unleash the power of mathematical reasoning. As we embark on this journey, we will uncover the hidden patterns and principles that govern the derivative of this unique expression. Through a combination of intuitive insights and systematic techniques, we will demystify the process and equip ourselves with a powerful tool for tackling complex mathematical problems.
So, fasten your seatbelts and prepare to delve into the captivating world of calculus, where the derivative of xy factorial awaits with its mind-blowing secret. By the end of this journey, you will not only grasp the intricacies of this remarkable concept but also gain a deeper appreciation for the elegance and precision of mathematical reasoning. Let's embark on this exhilarating adventure and unlock the secrets that lie within the derivative of xy factorial!
Read more: How To Find The Derivative Of A Graph
Understanding the Derivative of xy!
The derivative of xy factorial, denoted as (xy)!, is a captivating mathematical puzzle that beckons us to unravel its intricacies. To comprehend this enigmatic expression, let's break it down into its fundamental components. The concept of factorials, denoted by the exclamation mark, represents the product of all positive integers up to a given number. In the case of xy factorial, we are multiplying all positive integers from xy down to 1.
When we delve into the realm of calculus, the derivative represents the rate of change or the slope of a function at a specific point. In the context of xy factorial, finding its derivative involves applying the principles of differentiation to unveil the underlying pattern governing its rate of change.
To embark on this mathematical quest, we must harness the power of the product rule, a fundamental technique in calculus that enables us to differentiate the product of two functions. By applying the product rule to the expression xy!, we can systematically unravel the derivative of this intriguing factorial.
The product rule states that the derivative of the product of two functions, u(x) and v(x), is given by the formula u'(x)v(x) + u(x)v'(x), where u'(x) and v'(x) represent the derivatives of the respective functions. Applying this rule to xy!, we can discern the mesmerizing pattern that governs its derivative.
As we navigate through the intricacies of differentiation, we encounter the captivating interplay between the variables x and y, each contributing to the derivative in a unique and harmonious manner. Unveiling the derivative of xy! involves a delicate dance of mathematical reasoning, where the product rule serves as our guiding light through the labyrinth of calculus.
By understanding the derivative of xy factorial, we not only unravel the mysteries of its rate of change but also gain valuable insights into the elegance and precision of mathematical reasoning. This journey through the derivative of xy! equips us with a profound understanding of the intricate relationships between variables and the mesmerizing patterns that govern their transformations.
As we continue our expedition into the realm of calculus, armed with the knowledge of the derivative of xy!, we are poised to tackle complex problems and unlock the secrets that lie within the fabric of mathematical reality. Let's harness this newfound understanding as we venture into the application of the mind-blowing secret in our exploration of calculus and its far-reaching implications.
Applying the Mind-Blowing Secret
Armed with a profound understanding of the derivative of xy factorial, we are now ready to apply the mind-blowing secret that unlocks the hidden potential of this captivating expression. The application of this secret not only illuminates the intricate relationships between variables but also empowers us to unravel the mysteries of change and transformation in the realm of calculus.
As we delve into the application of the mind-blowing secret, we are poised to encounter a diverse array of mathematical scenarios where the derivative of xy! plays a pivotal role. Whether it's in the context of modeling real-world phenomena, optimizing functions, or unraveling the dynamics of complex systems, the mind-blowing secret serves as our compass through the uncharted territories of calculus.
One of the remarkable applications of the mind-blowing secret lies in the realm of optimization, where we seek to find the maximum or minimum values of a function. By leveraging the derivative of xy factorial and applying the principles of optimization, we can unravel the optimal configurations that yield the most favorable outcomes. This empowers us to tackle real-world problems with precision and insight, from maximizing the efficiency of a manufacturing process to minimizing the cost of production.
Furthermore, the mind-blowing secret paves the way for us to explore the dynamics of change and growth in various contexts. Whether it's analyzing the population growth of a species, modeling the spread of a contagious disease, or understanding the trajectory of a projectile, the derivative of xy! serves as a powerful tool for unraveling the underlying patterns of transformation and variation.
In the realm of physics, the mind-blowing secret finds profound applications in unraveling the intricacies of motion, energy, and forces. By harnessing the derivative of xy factorial, we can dissect the velocity, acceleration, and momentum of objects in motion, shedding light on the fundamental principles that govern the physical world.
As we navigate through these diverse applications, the mind-blowing secret unveils the profound impact of the derivative of xy factorial in shaping our understanding of the world around us. Its applications span across a myriad of disciplines, from engineering and economics to biology and physics, enriching our comprehension of the intricate tapestry of mathematical reasoning.
In essence, the application of the mind-blowing secret transcends the boundaries of traditional calculus, propelling us into a realm where the derivative of xy! becomes a catalyst for innovation, discovery, and profound insights. By harnessing this secret, we embark on a transformative journey that not only enriches our mathematical prowess but also deepens our appreciation for the boundless potential of calculus in unraveling the mysteries of the universe.
Examples and Applications
The derivative of xy factorial, a seemingly enigmatic expression, unfolds a rich tapestry of examples and applications that permeate diverse realms of mathematics and real-world scenarios. As we embark on this exploration, we encounter a myriad of captivating instances where the derivative of xy! serves as a powerful tool for unraveling the mysteries of change, transformation, and optimization.
Optimizing Production Processes
In the domain of manufacturing and production, the derivative of xy! finds profound applications in optimizing processes to maximize efficiency and minimize costs. By leveraging the mind-blowing secret, engineers and analysts can delve into the intricate dynamics of production systems, identifying the optimal configurations that lead to enhanced productivity and reduced resource utilization. Whether it's streamlining assembly lines, fine-tuning inventory management, or optimizing supply chain logistics, the derivative of xy factorial serves as a guiding light in the quest for operational excellence.
Modeling Population Growth
The study of population dynamics and growth patterns unveils yet another compelling application of the mind-blowing secret. By applying the derivative of xy! to model population growth, researchers and demographers gain invaluable insights into the rate of change and the underlying factors driving demographic shifts. Whether it's analyzing the expansion of urban centers, projecting the growth of species in ecological systems, or understanding the implications of demographic transitions, the derivative of xy factorial offers a powerful lens through which to unravel the complex interplay of birth rates, mortality rates, and migration patterns.
Unraveling Projectile Motion
In the realm of physics and engineering, the derivative of xy factorial emerges as a cornerstone for understanding the dynamics of projectile motion. By harnessing the mind-blowing secret, physicists and engineers can dissect the trajectory, velocity, and acceleration of projectiles in flight, shedding light on the fundamental principles that govern the motion of objects through space. Whether it's calculating the optimal launch angles for projectiles, analyzing the behavior of projectiles in varying gravitational fields, or designing trajectories for space missions, the derivative of xy! stands as a fundamental tool for unraveling the intricacies of motion and dynamics.
Enhancing Financial Modeling
The derivative of xy factorial extends its reach into the domain of finance and economics, where it serves as a potent instrument for enhancing financial modeling and risk analysis. By applying the mind-blowing secret to model financial derivatives, analysts and economists gain a nuanced understanding of the rate of change in financial instruments, enabling them to assess and mitigate risks in investment portfolios, hedge against market fluctuations, and optimize investment strategies. Whether it's modeling the behavior of complex financial derivatives, analyzing the impact of interest rate changes, or forecasting the dynamics of financial markets, the derivative of xy! empowers financial experts to navigate the intricate landscape of economic phenomena with precision and insight.
In essence, the examples and applications of the derivative of xy factorial transcend disciplinary boundaries, permeating diverse domains with their profound impact and far-reaching implications. From optimizing production processes to unraveling population dynamics, from dissecting projectile motion to enhancing financial modeling, the mind-blowing secret unfolds a captivating tapestry of mathematical and real-world scenarios where the derivative of xy! serves as a catalyst for innovation, discovery, and profound insights.
Conclusion
In conclusion, the journey into the realm of the derivative of xy factorial has been nothing short of exhilarating. We embarked on this expedition with the goal of unraveling the mind-blowing secret that governs the rate of change of this captivating expression. Through our exploration, we have gained a profound understanding of the derivative of xy!, delving into its intricacies, applications, and far-reaching implications.
Our quest led us to unravel the hidden patterns and principles that govern the derivative of xy factorial, shedding light on the mesmerizing interplay between variables and the profound impact of differentiation in calculus. We harnessed the power of the product rule, a fundamental technique in calculus, to systematically unveil the derivative of xy factorial, unraveling its underlying structure and the captivating dynamics of change and transformation.
As we ventured further, we applied the mind-blowing secret to a diverse array of examples and applications, spanning realms such as optimization, population dynamics, projectile motion, and financial modeling. In each scenario, the derivative of xy! emerged as a potent tool for unraveling the mysteries of change, guiding us through the complexities of real-world phenomena, and empowering us to innovate, discover, and gain profound insights into the intricate tapestry of mathematical reasoning.
Our journey into the derivative of xy factorial has not only enriched our mathematical prowess but has also deepened our appreciation for the boundless potential of calculus in unraveling the mysteries of the universe. It has equipped us with a transformative understanding of the intricate relationships between variables, the mesmerizing patterns that govern their transformations, and the profound impact of differentiation in diverse disciplines.
As we conclude this expedition, we carry with us a newfound appreciation for the elegance and precision of mathematical reasoning, the far-reaching applications of the mind-blowing secret, and the boundless potential of the derivative of xy factorial in shaping our understanding of the world around us. Our journey serves as a testament to the captivating allure of mathematics, where the derivative of xy! stands as a beacon of insight, discovery, and infinite possibilities.
In essence, the derivative of xy factorial, with its mind-blowing secret, invites us to embark on a transformative journey, where the mysteries of change, transformation, and optimization converge to illuminate the profound beauty and power of mathematical reasoning. As we bid farewell to this expedition, we carry with us the enduring legacy of the derivative of xy!, a timeless enigma that continues to captivate and inspire the curious minds of mathematicians, scientists, and explorers of the unknown.