Home>Mathematics>The Simple Trick To Convert 13/15 To A Percentage In Seconds!
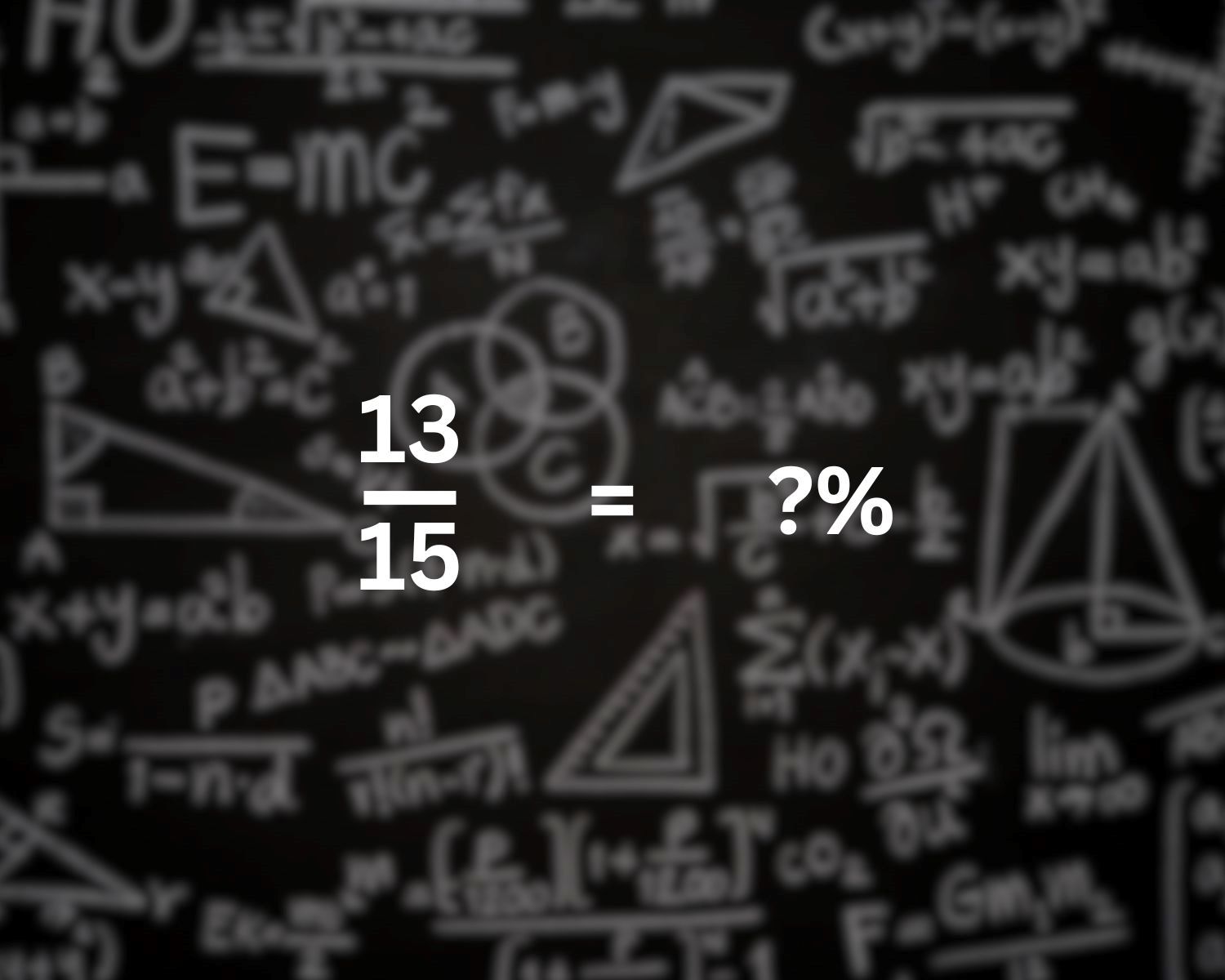
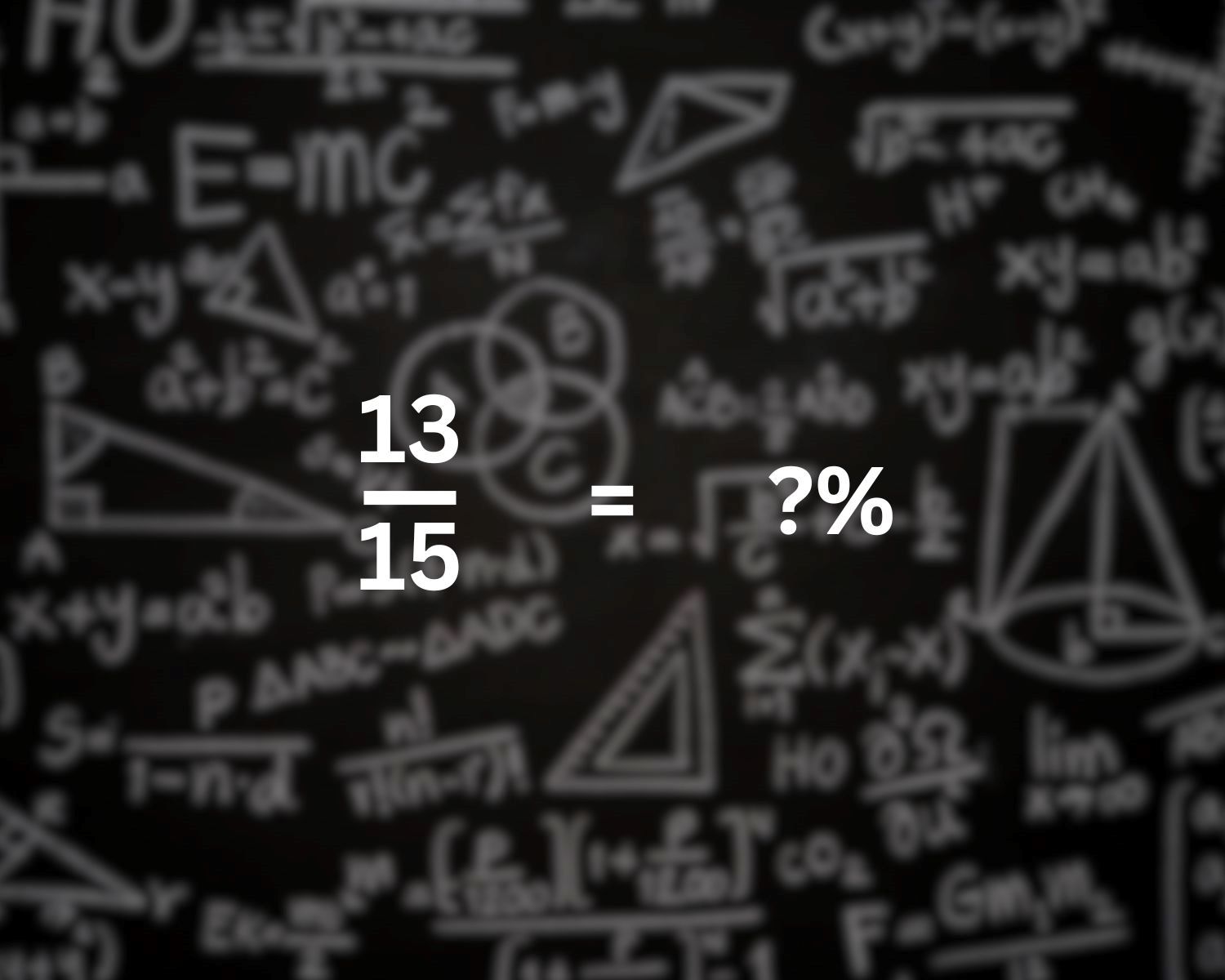
Mathematics
The Simple Trick To Convert 13/15 To A Percentage In Seconds!
Published: February 20, 2024
Learn the simple trick to convert 13/15 to a percentage in seconds! Master mathematics with this quick and easy method.
(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)
Table of Contents
Introduction
Understanding the concept of converting fractions to percentages is a fundamental skill in mathematics. It allows us to express fractions in a more relatable and practical form, making it easier to compare and work with different values. In this article, we will delve into the simple trick to convert the fraction 13/15 to a percentage in seconds. By mastering this technique, you will gain a valuable tool for quick and accurate percentage conversions, empowering you to tackle a wide range of mathematical problems with confidence.
Converting fractions to percentages is a common task in everyday life, from calculating discounts during shopping to understanding proportions in recipes. It's a skill that transcends the boundaries of the classroom, finding practical applications in various real-world scenarios. By grasping the concept and the simple trick involved, you can streamline your approach to solving problems that involve percentages, making the process more intuitive and efficient.
The ability to convert fractions to percentages is not only practical but also empowers individuals to make informed decisions based on numerical data. Whether it's analyzing financial reports, interpreting statistical information, or understanding trends in data analysis, the skill of converting fractions to percentages is a valuable asset in a wide range of professional and personal contexts.
In the following sections, we will explore the underlying principles of converting fractions to percentages and unveil the simple trick that will enable you to perform this conversion effortlessly. Through clear explanations and illustrative examples, you will gain a deeper understanding of the process and develop the confidence to apply this knowledge in various mathematical and real-world scenarios. Let's embark on this journey to unravel the simplicity behind converting 13/15 to a percentage in seconds and equip ourselves with a valuable mathematical tool.
Understanding the concept of converting fractions to percentages
Converting fractions to percentages is a fundamental skill that allows us to express fractional values in a more relatable and practical form. This process involves transforming a fraction into its equivalent percentage, which represents a proportion of 100. By understanding the concept behind this conversion, we can gain valuable insights into the relative magnitude of a fraction in relation to the whole.
To comprehend the conversion from fractions to percentages, it is essential to grasp the underlying relationship between these two numerical representations. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (the top number) denotes the part, while the denominator (the bottom number) signifies the whole. On the other hand, a percentage represents a portion of 100, providing a standardized way to compare values relative to the whole.
When converting a fraction to a percentage, we are essentially expressing the fractional value as a proportion of 100. This transformation allows us to gauge the significance of the fraction in a standardized format, making it easier to compare with other percentages and numerical values. The process of converting a fraction to a percentage involves multiplying the fraction by 100, resulting in a numerical representation that reflects its proportion out of 100.
Understanding the concept of converting fractions to percentages enables us to interpret numerical data more effectively. It equips us with the ability to express fractional values in a format that is widely used for comparison, analysis, and decision-making. Whether it's evaluating proportions in statistical data, calculating markup or discount percentages in business, or interpreting ratios in everyday scenarios, the skill of converting fractions to percentages is a versatile tool with practical applications across various domains.
By mastering this concept, individuals can enhance their numerical literacy and make informed judgments based on percentage representations. It provides a framework for comprehending relative magnitudes and proportions, fostering a deeper understanding of numerical relationships. Moreover, the ability to convert fractions to percentages empowers individuals to communicate numerical information more effectively, facilitating clear and concise expression of proportions and comparisons.
In the subsequent section, we will explore a simple trick to convert the fraction 13/15 to a percentage in seconds, building upon the foundational understanding of converting fractions to percentages. This practical technique will streamline the process of percentage conversion, enabling quick and accurate calculations that can be applied to a wide range of mathematical and real-world scenarios. Let's delve into this simple yet powerful method to convert fractions to percentages with ease and confidence.
The simple trick to convert 13/15 to a percentage in seconds
Converting the fraction 13/15 to a percentage can be accomplished with a simple and efficient technique. The key to this method lies in recognizing that the percentage value is obtained by multiplying the fraction by 100. By applying this straightforward approach, we can swiftly transform the given fraction into its equivalent percentage representation.
To convert 13/15 to a percentage, we can follow these steps:
-
Multiply the fraction by 100: Begin by multiplying the fraction 13/15 by 100. This step effectively scales the fraction to represent its proportion out of 100, yielding the percentage value.
[ frac{13}{15} times 100 = frac{13 times 100}{15} = frac{1300}{15} ]
-
Simplify the fraction (if necessary): The resulting fraction, 1300/15, can be simplified to its lowest terms to obtain the final percentage value. In this case, the fraction simplifies to 86.67, which can be rounded to 86.67% or expressed as 86.67 percent.
By following these steps, we can efficiently convert the fraction 13/15 to the percentage value of 86.67%. This simple trick allows us to perform the conversion in a matter of seconds, providing a quick and reliable method to express the given fraction in a percentage format.
This technique can be applied to a wide range of fractions, enabling rapid conversion to percentage values with ease. By understanding and mastering this simple trick, individuals can streamline their approach to percentage calculations, making the process more intuitive and efficient.
The ability to convert fractions to percentages in seconds empowers individuals to tackle numerical problems with confidence and precision. Whether it's determining proportions, analyzing data, or interpreting real-world scenarios involving percentages, this practical technique serves as a valuable tool for quick and accurate percentage conversions.
In the subsequent section, we will explore examples of converting other fractions to percentages using the same simple trick, further demonstrating the versatility and effectiveness of this approach. By applying this method to various fractions, we can gain a deeper appreciation for its simplicity and utility in converting fractions to percentages seamlessly. Let's embark on this exploration to expand our proficiency in converting fractions to percentages using the simple trick.
Examples of converting other fractions to percentages using the same trick
Let's explore the application of the simple trick to convert various fractions to percentages, showcasing its versatility and effectiveness across different numerical values. By applying the straightforward method of multiplying the fraction by 100, we can swiftly obtain the equivalent percentage representation, enabling quick and accurate conversions.
Example 1: Converting 3/4 to a percentage
To convert the fraction 3/4 to a percentage, we can follow the same simple trick:
- Multiply the fraction by 100:
[ frac{3}{4} times 100 = frac{3 times 100}{4} = frac{300}{4} ] - Simplify the fraction (if necessary):
The resulting fraction, 300/4, simplifies to 75. Therefore, 3/4 is equivalent to 75%.
Example 2: Converting 5/8 to a percentage
Applying the simple trick to convert the fraction 5/8 to a percentage:
- Multiply the fraction by 100:
[ frac{5}{8} times 100 = frac{5 times 100}{8} = frac{500}{8} ] - Simplify the fraction (if necessary):
The resulting fraction, 500/8, simplifies to 62.5. Hence, 5/8 is equivalent to 62.5%.
Example 3: Converting 7/10 to a percentage
Using the same method to convert the fraction 7/10 to a percentage:
- Multiply the fraction by 100:
[ frac{7}{10} times 100 = frac{7 times 100}{10} = frac{700}{10} ] - Simplify the fraction (if necessary):
The resulting fraction, 700/10, simplifies to 70. Therefore, 7/10 is equivalent to 70%.
Example 4: Converting 2/3 to a percentage
Applying the simple trick to convert the fraction 2/3 to a percentage:
- Multiply the fraction by 100:
[ frac{2}{3} times 100 = frac{2 times 100}{3} = frac{200}{3} ] - Simplify the fraction (if necessary):
The resulting fraction, 200/3, is approximately 66.67 when rounded. Hence, 2/3 is approximately 66.67%.
By showcasing these examples, we demonstrate the consistent application of the simple trick to convert various fractions to percentages. This method offers a quick and reliable approach to obtain percentage representations of different fractions, empowering individuals to perform percentage conversions with ease and confidence. The versatility of this technique extends to a wide range of fractions, making it a valuable tool for numerical calculations and real-world applications.
In summary, the simple trick of multiplying the fraction by 100 provides a seamless and efficient method for converting fractions to percentages, enabling individuals to navigate numerical problems with precision and agility. This practical approach enhances numerical literacy and equips individuals with a valuable skill for interpreting and expressing fractional values in percentage format.
Conclusion
In conclusion, the ability to convert fractions to percentages is a fundamental skill that holds significant practical value in various contexts, from academic settings to real-world applications. By understanding the concept of converting fractions to percentages and mastering the simple trick of multiplying the fraction by 100, individuals can streamline the process of percentage calculations, enabling quick and accurate conversions with ease.
The simple trick of converting fractions to percentages in seconds empowers individuals to navigate numerical problems with confidence and precision. It provides a practical approach to express fractional values in a standardized format, making it easier to compare, analyze, and interpret numerical data. This proficiency in percentage conversions extends beyond the realm of mathematics, finding relevance in everyday scenarios such as shopping discounts, financial analysis, and statistical interpretations.
By applying the simple trick to convert fractions to percentages, individuals can enhance their numerical literacy and make informed decisions based on percentage representations. This skill fosters a deeper understanding of relative magnitudes and proportions, enabling clear and concise expression of numerical information. Moreover, the ability to swiftly convert fractions to percentages equips individuals with a valuable tool for interpreting proportions, analyzing data, and making informed judgments based on percentage values.
The examples presented in this article demonstrate the versatility and effectiveness of the simple trick in converting various fractions to percentages. By showcasing the consistent application of this method across different numerical values, we illustrate its practical utility and relevance in diverse mathematical and real-world scenarios. This proficiency in percentage conversions not only simplifies mathematical calculations but also fosters a deeper appreciation for numerical relationships and proportions.
In essence, the simple trick to convert fractions to percentages in seconds serves as a valuable asset for individuals seeking to enhance their mathematical skills and numerical literacy. By mastering this technique, individuals can approach percentage calculations with ease and efficiency, gaining a deeper understanding of numerical proportions and their practical implications. This proficiency extends beyond the confines of the classroom, offering a practical tool for interpreting and expressing numerical data in percentage format, thereby empowering individuals to make informed decisions based on clear and standardized representations of proportions.
In embracing the simplicity and effectiveness of the simple trick, individuals can elevate their proficiency in percentage conversions, unlocking a valuable skill that transcends mathematical exercises and finds relevance in everyday decision-making and analysis. The journey to unravel the simplicity behind converting fractions to percentages in seconds equips individuals with a practical and empowering tool, fostering confidence and precision in navigating numerical challenges and real-world scenarios.