How To Determine The End Behavior Of A Function

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)

Introduction

Understanding the behavior of mathematical functions is crucial in various fields, from engineering to economics. One essential aspect of a function's behavior is its end behavior, which provides insights into how the function behaves as the input values approach positive or negative infinity. By analyzing the end behavior, mathematicians and scientists can make predictions about the long-term trends and characteristics of functions.

In this article, we will delve into the concept of end behavior and explore how it applies to different types of functions, including polynomial, rational, exponential, and logarithmic functions. By understanding the end behavior of these functions, you will gain valuable insights into their overall trends and tendencies, enabling you to make informed decisions and predictions in real-world scenarios.

Let's embark on a journey to unravel the mysteries of end behavior and equip ourselves with the knowledge to analyze and interpret the behavior of various mathematical functions. Whether you're a student delving into the depths of calculus or a professional seeking to apply mathematical principles in your field, understanding end behavior is a fundamental skill that will enrich your problem-solving abilities and analytical prowess.

Understanding End Behavior

End behavior refers to the behavior of a function as the input values approach positive or negative infinity. It provides crucial insights into the long-term trends and characteristics of a function, offering valuable information for making predictions and analyzing its overall behavior. By understanding end behavior, mathematicians and scientists can gain a deeper understanding of how functions behave in the far-reaching realms of the input domain.

When analyzing the end behavior of a function, it is essential to consider the leading term of the function's equation. The leading term, often the term with the highest degree in the function, dictates the dominant behavior of the function as the input values become extremely large or small. By focusing on the leading term, mathematicians can discern whether the function grows without bound, approaches a specific value, oscillates, or exhibits other distinct behaviors in the long run.

In the context of polynomial functions, the end behavior is determined by the degree and leading coefficient of the polynomial. For rational functions, the end behavior is influenced by the degrees of the numerator and denominator, leading to different behaviors such as horizontal asymptotes or oblique asymptotes. Exponential functions showcase distinct end behavior patterns, with exponential growth or decay dominating the function's long-term behavior. Similarly, logarithmic functions exhibit unique end behavior characteristics, reflecting the asymptotic nature of logarithmic growth or decay.

Understanding end behavior empowers mathematicians and analysts to make informed predictions about the behavior of functions in real-world scenarios. Whether modeling population growth, analyzing economic trends, or predicting the decay of radioactive substances, the ability to interpret end behavior provides a powerful tool for making accurate projections and understanding the fundamental nature of mathematical functions.

In summary, end behavior serves as a window into the far-reaching tendencies of functions, shedding light on their behavior as the input values extend towards infinity or negative infinity. By grasping the concept of end behavior and its implications for different types of functions, individuals can harness the predictive power of mathematics to gain deeper insights into the behavior of various phenomena, ultimately enriching their analytical skills and problem-solving capabilities.

Determining End Behavior for Polynomial Functions

Polynomial functions, characterized by their algebraic expressions involving variables raised to non-negative integer powers, exhibit distinct end behavior patterns determined by the degree and leading coefficient of the polynomial. Understanding the end behavior of polynomial functions is essential for gaining insights into their long-term trends and characteristics.

Degree and Leading Coefficient

The end behavior of a polynomial function is primarily influenced by its degree, which corresponds to the highest power of the variable in the function's algebraic expression. Additionally, the leading coefficient, representing the coefficient of the term with the highest degree, plays a pivotal role in shaping the function's behavior as the input values extend towards positive or negative infinity.

Odd Degree Polynomials

For polynomial functions with an odd degree, the end behavior diverges in opposite directions as the input values approach positive and negative infinity. When the leading coefficient is positive, the function rises to positive infinity for large positive input values and descends to negative infinity for large negative input values. Conversely, if the leading coefficient is negative, the function descends to negative infinity for large positive input values and rises to positive infinity for large negative input values.

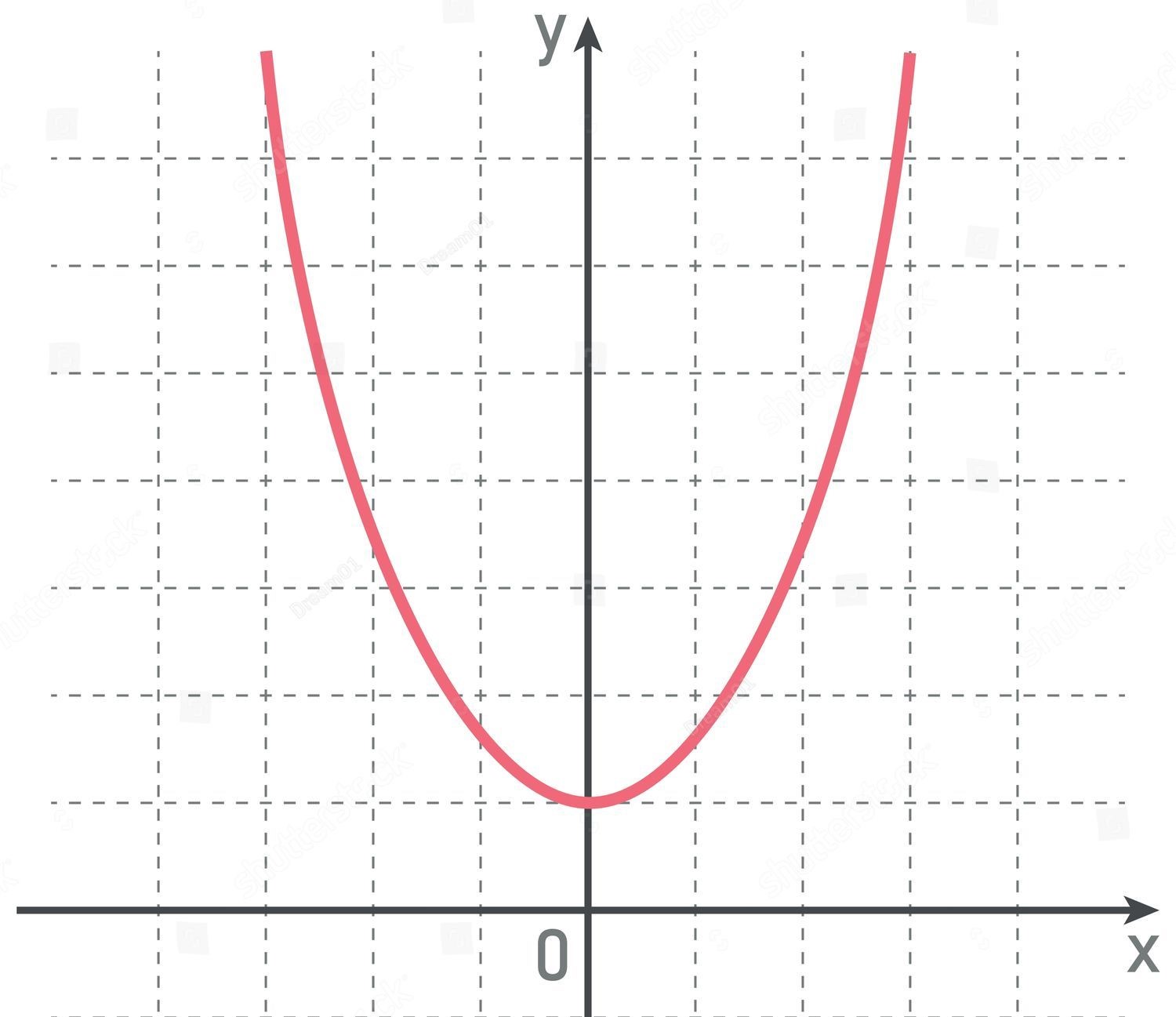
Even Degree Polynomials

In contrast, polynomial functions with an even degree exhibit similar end behavior trends as the input values extend towards positive and negative infinity. When the leading coefficient is positive, the function rises to positive infinity for both large positive and negative input values. Conversely, if the leading coefficient is negative, the function descends to negative infinity for both large positive and negative input values.

Horizontal Asymptotes

In some cases, polynomial functions may feature horizontal asymptotes, which are horizontal lines that the function approaches as the absolute value of the input values becomes arbitrarily large. The presence of horizontal asymptotes indicates specific long-term behavior for the function, offering valuable insights into its end behavior characteristics.

By analyzing the degree and leading coefficient of polynomial functions, mathematicians and analysts can determine their end behavior and make informed predictions about their long-term trends. Whether modeling natural phenomena, economic trends, or physical processes, understanding the end behavior of polynomial functions equips individuals with a powerful tool for interpreting and predicting the behavior of diverse real-world phenomena.

In summary, the end behavior of polynomial functions is intricately linked to their degree and leading coefficient, shaping their long-term trends and providing valuable insights into their behavior as the input values extend towards positive or negative infinity. By mastering the art of determining the end behavior of polynomial functions, individuals can unlock the predictive potential of mathematics and gain a deeper understanding of the fundamental nature of polynomial expressions.

Determining End Behavior for Rational Functions

Rational functions, defined as the quotient of two polynomial functions, exhibit unique end behavior characteristics that offer valuable insights into their long-term trends and behavior as the input values approach positive or negative infinity. Understanding the end behavior of rational functions is essential for mathematicians and analysts seeking to interpret and predict the behavior of diverse real-world phenomena modeled by these functions.

The end behavior of a rational function is primarily influenced by the degrees of the numerator and denominator polynomials. By examining these degrees, mathematicians can discern the dominant behavior of the rational function as the input values extend towards positive or negative infinity. Additionally, the presence of horizontal or oblique asymptotes further shapes the end behavior of rational functions, providing crucial information for making predictions and analyzing their overall trends.

When analyzing the end behavior of rational functions, mathematicians consider the relative degrees of the numerator and denominator. If the degree of the numerator is less than the degree of the denominator, the rational function exhibits a horizontal asymptote at y = 0. This indicates that as the input values become extremely large or small, the function approaches the x-axis, reflecting its long-term behavior and tendencies.

Conversely, if the degree of the numerator is equal to the degree of the denominator, the rational function features a horizontal asymptote determined by the ratio of the leading coefficients of the numerator and denominator. This horizontal asymptote provides insights into the long-term behavior of the function, guiding mathematicians in making predictions and interpretations based on its end behavior characteristics.

In some cases, rational functions may exhibit oblique asymptotes, characterized by non-horizontal straight lines that the function approaches as the absolute value of the input values becomes arbitrarily large. The presence of oblique asymptotes indicates specific long-term behavior for the function, offering valuable insights into its end behavior characteristics and enabling mathematicians to make informed predictions about its behavior in real-world scenarios.

By understanding the end behavior of rational functions, mathematicians and analysts can gain valuable insights into their long-term trends and characteristics. Whether modeling economic trends, analyzing population dynamics, or predicting the behavior of physical systems, the ability to interpret the end behavior of rational functions equips individuals with a powerful tool for making accurate projections and understanding the fundamental nature of these mathematical expressions.

In summary, the end behavior of rational functions is intricately linked to the degrees of the numerator and denominator, as well as the presence of horizontal or oblique asymptotes. By mastering the art of determining the end behavior of rational functions, individuals can unlock the predictive potential of mathematics and gain a deeper understanding of the fundamental nature of these essential mathematical expressions.

Determining End Behavior for Exponential Functions

Exponential functions, characterized by their algebraic expressions in the form of f(x) = a^x, where 'a' is a positive real number, exhibit distinctive end behavior patterns that provide valuable insights into their long-term trends and behavior as the input values approach positive or negative infinity. Understanding the end behavior of exponential functions is essential for mathematicians and analysts seeking to interpret and predict the behavior of diverse real-world phenomena modeled by these functions.

The end behavior of exponential functions is primarily determined by the value of the base 'a'. When the base 'a' is greater than 1, the exponential function experiences exponential growth as the input values extend towards positive infinity. This growth behavior signifies that the function rises rapidly, approaching positive infinity as the input values become increasingly large. Conversely, as the input values approach negative infinity, the function approaches zero but never actually reaches it, demonstrating its unbounded growth in the positive direction.

On the other hand, when the base 'a' is between 0 and 1, the exponential function undergoes exponential decay as the input values extend towards positive infinity. In this scenario, the function decreases rapidly, approaching zero as the input values become increasingly large. As the input values approach negative infinity, the function rises towards positive infinity but never actually reaches it, showcasing its unbounded decay in the positive direction.

The behavior of exponential functions as the input values approach positive or negative infinity is characterized by their unbounded growth or decay, providing crucial insights into their long-term trends and tendencies. By understanding the end behavior of exponential functions, mathematicians and analysts can make informed predictions about their behavior in real-world scenarios, ranging from population growth models to the decay of radioactive substances.

In summary, the end behavior of exponential functions is intricately linked to the value of the base 'a', dictating whether the function exhibits exponential growth or decay as the input values extend towards positive or negative infinity. By mastering the art of determining the end behavior of exponential functions, individuals can unlock the predictive potential of mathematics and gain a deeper understanding of the fundamental nature of these essential mathematical expressions.

Determining End Behavior for Logarithmic Functions

Logarithmic functions, represented by algebraic expressions in the form of f(x) = log_b(x), where 'b' is the base of the logarithm, exhibit unique end behavior characteristics that offer valuable insights into their long-term trends and behavior as the input values approach positive or negative infinity. Understanding the end behavior of logarithmic functions is essential for mathematicians and analysts seeking to interpret and predict the behavior of diverse real-world phenomena modeled by these functions.

The end behavior of logarithmic functions is primarily determined by the base 'b' of the logarithm. When the base 'b' is greater than 1, the logarithmic function experiences logarithmic growth as the input values extend towards positive infinity. In this scenario, the function rises slowly, approaching positive infinity as the input values become increasingly large. As the input values approach zero from the positive side, the function approaches negative infinity, showcasing its unbounded growth in the negative direction.

Conversely, when the base 'b' is between 0 and 1, the logarithmic function undergoes logarithmic decay as the input values extend towards positive infinity. The function decreases slowly, approaching negative infinity as the input values become increasingly large. As the input values approach zero from the positive side, the function approaches positive infinity, demonstrating its unbounded decay in the positive direction.

The behavior of logarithmic functions as the input values approach positive or negative infinity is characterized by their unbounded growth or decay, providing crucial insights into their long-term trends and tendencies. By understanding the end behavior of logarithmic functions, mathematicians and analysts can make informed predictions about their behavior in real-world scenarios, ranging from analyzing the diminishing returns in economic models to understanding the diminishing impact of additional resources in various fields.

In summary, the end behavior of logarithmic functions is intricately linked to the base 'b', dictating whether the function exhibits logarithmic growth or decay as the input values extend towards positive or negative infinity. By mastering the art of determining the end behavior of logarithmic functions, individuals can unlock the predictive potential of mathematics and gain a deeper understanding of the fundamental nature of these essential mathematical expressions.

Conclusion

In conclusion, the concept of end behavior serves as a powerful tool for understanding the long-term trends and characteristics of various mathematical functions. By analyzing the behavior of functions as the input values approach positive or negative infinity, mathematicians and analysts can make informed predictions, interpret real-world phenomena, and gain valuable insights into the fundamental nature of mathematical expressions.

Throughout this exploration, we have delved into the intricacies of end behavior for different types of functions, including polynomial, rational, exponential, and logarithmic functions. Each category of functions exhibits unique end behavior patterns, shaped by their degree, leading coefficient, base, and other defining characteristics. By understanding the end behavior of these functions, individuals can unlock the predictive potential of mathematics and apply their insights to diverse fields, ranging from economics and engineering to the natural sciences and beyond.

The end behavior of polynomial functions, influenced by their degree and leading coefficient, provides valuable insights into their long-term trends and tendencies. Whether exhibiting exponential growth, decay, or approaching specific values, polynomial functions showcase diverse end behavior patterns that enable mathematicians to make accurate projections and interpretations in various contexts.

Rational functions, characterized by their numerator and denominator degrees, offer distinct end behavior characteristics, including horizontal and oblique asymptotes. By understanding the relative degrees of the numerator and denominator, mathematicians can discern the dominant behavior of rational functions as the input values extend towards positive or negative infinity, enriching their ability to interpret and predict real-world phenomena modeled by these functions.

Exponential functions, defined by their base, exhibit exponential growth or decay as the input values approach positive or negative infinity. The behavior of exponential functions provides crucial insights into phenomena such as population growth, decay processes, and other exponential trends, empowering mathematicians to make informed predictions and interpretations in diverse fields.

Logarithmic functions, determined by their base, showcase logarithmic growth or decay as the input values extend towards positive or negative infinity. By understanding the end behavior of logarithmic functions, individuals can gain valuable insights into phenomena such as diminishing returns, resource allocation, and other logarithmic trends, enhancing their ability to interpret and predict real-world scenarios.

In essence, the exploration of end behavior for different types of functions equips individuals with a deeper understanding of the fundamental nature of mathematical expressions. By mastering the art of determining end behavior, mathematicians and analysts can harness the predictive potential of mathematics, making accurate projections and interpretations in diverse fields, ultimately enriching their problem-solving abilities and analytical prowess.