Discover The Secret To Finding The Height Of A Cylinder With Just The Volume And Radius!

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)

Introduction

Welcome to the fascinating world of cylinders and the intriguing mathematics that govern their dimensions. Have you ever pondered over the question of how to determine the height of a cylinder solely based on its volume and radius? This enigma has captivated the minds of mathematicians and scientists for centuries, leading to the development of ingenious formulas that unlock the secrets hidden within these three-dimensional shapes.

In this article, we will embark on a journey of discovery, delving into the intricacies of cylinders and unraveling the mystery of finding their height with just the volume and radius at our disposal. Through a blend of logic, creativity, and mathematical prowess, we will explore the fundamental concepts that underpin the volume of a cylinder and the intricate relationship between its dimensions.

Prepare to be amazed as we navigate through the realm of geometric wonders, where the enigmatic nature of cylinders is demystified through the lens of mathematical reasoning. By the end of our exploration, you will possess the knowledge and tools to confidently decipher the height of a cylinder, armed with nothing more than its volume and radius.

So, let's embark on this mathematical odyssey, where the allure of cylinders beckons us to uncover their hidden dimensions and embrace the elegance of mathematical reasoning. Join me as we venture into the heart of this geometric conundrum and emerge enlightened with the key to unraveling the height of a cylinder, unlocking a realm of mathematical marvels that await our discovery.

Understanding the Volume of a Cylinder

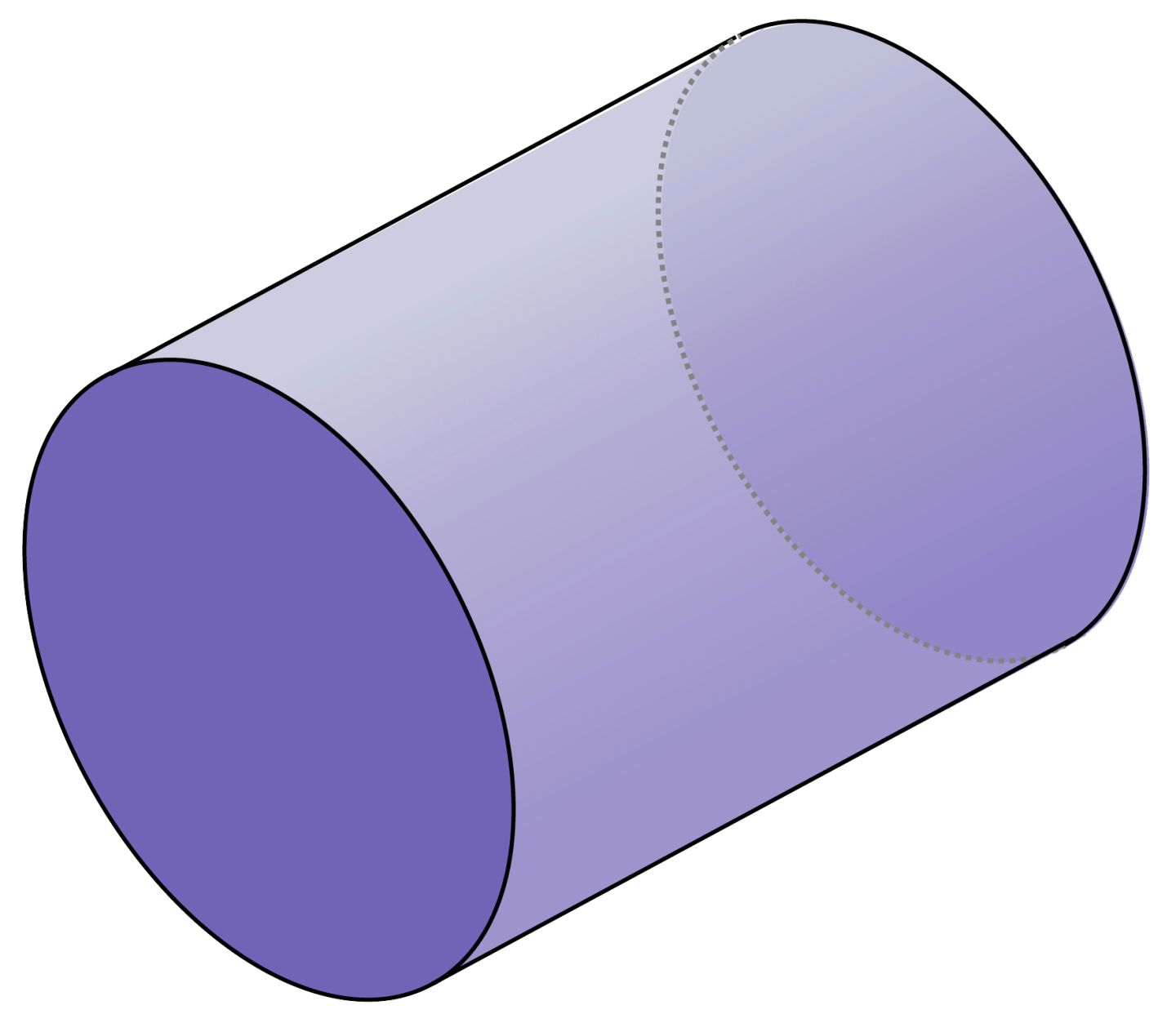
The volume of a cylinder is a fundamental concept in geometry, representing the amount of space enclosed within its three-dimensional structure. To comprehend the volume of a cylinder, it is essential to visualize the cylinder as a solid figure with two congruent circular bases connected by a curved surface. This distinctive shape gives rise to a specific method for calculating its volume, setting it apart from other geometric forms.

The formula for determining the volume of a cylinder is derived from the area of its circular base and the height of the cylinder. By envisioning the cylinder as a stack of circular discs, each with an infinitesimally small thickness, the concept of volume becomes tangible. When these discs are stacked together from the base to the top of the cylinder, they collectively form its volume.

Mathematically, the volume of a cylinder can be expressed as V = πr^2h, where V represents the volume, r denotes the radius of the circular base, and h signifies the height of the cylinder. This formula encapsulates the essence of the cylinder's volumetric properties, illustrating the interplay between its dimensions in a concise and elegant manner.

Understanding the volume of a cylinder entails grasping the relationship between the dimensions of its circular base and the height that extends perpendicular to this base. This interconnectedness forms the crux of the cylinder's volumetric nature, where the magnitude of its volume is intricately linked to the size of its base and the extent of its height.

By comprehending the volume of a cylinder, we gain insight into the spatial capacity it occupies, transcending mere numerical values to appreciate the geometric essence of this captivating shape. Through the lens of mathematical reasoning, the volume of a cylinder emerges as a testament to the harmonious fusion of its circular base and towering height, culminating in a unified representation of spatial magnitude.

In unraveling the intricacies of the volume of a cylinder, we lay the groundwork for delving deeper into its geometric properties, setting the stage for our exploration into the enigmatic realm of finding the height of a cylinder based solely on its volume and radius. This foundational understanding forms the bedrock of our quest to unlock the secrets concealed within the dimensions of a cylinder, paving the way for the revelation of its hidden height.

Understanding the Formula for the Volume of a Cylinder

The formula for determining the volume of a cylinder is a remarkable manifestation of mathematical elegance, encapsulating the essence of this three-dimensional shape in a concise and powerful expression. At the heart of this formula lies the intrinsic relationship between the dimensions of the cylinder, namely the radius of its circular base and the height that extends perpendicular to this base.

Mathematically, the volume of a cylinder is represented by the formula V = πr^2h, where V denotes the volume, r signifies the radius of the circular base, and h represents the height of the cylinder. This formula embodies the synergy between the geometric attributes of the cylinder, harmonizing the spatial magnitude enclosed within its curved boundaries with the dimensions of its base and height.

The significance of the radius, denoted by 'r', cannot be understated, as it serves as a pivotal determinant of the cylinder's volume. The squared value of the radius, represented by πr^2, corresponds to the area of the circular base. This foundational relationship underscores the pivotal role of the circular base in contributing to the volume of the cylinder, as the extent of its spatial occupation is intricately linked to the magnitude of the radius.

Furthermore, the height of the cylinder, symbolized by 'h', stands as a defining factor in the determination of its volume. By multiplying the area of the circular base (πr^2) with the height (h), the formula encapsulates the vertical extent of the cylinder's volumetric capacity. This symbiotic interplay between the base and height illuminates the integral role of each dimension in shaping the overall volume of the cylinder, underscoring the interconnectedness of its geometric attributes.

In essence, the formula for the volume of a cylinder serves as a testament to the profound unity between its base and height, transcending numerical values to embody the geometric essence of this captivating shape. Through this formula, the intrinsic relationship between the radius, the height, and the resulting volume emerges as a testament to the harmonious fusion of geometric dimensions, unveiling the spatial magnitude encapsulated within the cylindrical confines.

As we unravel the intricacies of the formula for the volume of a cylinder, we gain a deeper appreciation for the geometric harmony that underpins its volumetric properties, setting the stage for our exploration into the enigmatic realm of finding the height of a cylinder based solely on its volume and radius. This foundational understanding forms the bedrock of our quest to unlock the secrets concealed within the dimensions of a cylinder, paving the way for the revelation of its hidden height.

Deriving the Formula for the Height of a Cylinder

The quest to derive the formula for the height of a cylinder based solely on its volume and radius beckons us to embark on a journey of mathematical ingenuity. At the crux of this endeavor lies the intricate interplay between the volumetric properties of the cylinder and the geometric dimensions that define its structure. To unlock the enigma of the cylinder's height, we must unravel the underlying relationships between its volume, radius, and height, culminating in a formula that encapsulates this profound connection.

Mathematically, the formula for the volume of a cylinder is expressed as V = πr^2h, where V represents the volume, r denotes the radius of the circular base, and h signifies the height of the cylinder. By manipulating this formula, we can derive an expression for the height of the cylinder in terms of its volume and radius. Through algebraic manipulation and logical reasoning, we can isolate the variable for height, unveiling a formula that unveils the hidden dimension of the cylinder.

By rearranging the formula for the volume of the cylinder, we can express the height 'h' in terms of the volume 'V' and the radius 'r' as follows:

[ h = frac{V}{pi r^2} ]

This elegant expression encapsulates the essence of the cylinder's height, linking it directly to the volumetric capacity enclosed within its curved boundaries and the magnitude of its circular base. The derivation of this formula represents a triumph of mathematical reasoning, as it unveils the intrinsic relationship between the volume, radius, and height of the cylinder in a succinct and powerful expression.

In essence, the formula for the height of a cylinder serves as a testament to the profound unity between its volumetric properties and geometric dimensions, transcending numerical values to embody the geometric essence of this captivating shape. Through this formula, the intrinsic relationship between the volume, the radius, and the resulting height emerges as a testament to the harmonious fusion of geometric dimensions, unveiling the spatial magnitude encapsulated within the cylindrical confines.

As we delve into the derivation of the formula for the height of a cylinder, we gain a deeper appreciation for the mathematical elegance that underpins its dimensional properties, setting the stage for our application of this formula to unlock the hidden height of a cylinder based solely on its volume and radius. This foundational understanding forms the bedrock of our quest to unveil the secrets concealed within the dimensions of a cylinder, paving the way for the revelation of its hidden height.

This derivation represents a triumph of mathematical reasoning, as it unveils the intrinsic relationship between the volume, radius, and height of the cylinder in a succinct and powerful expression.

Applying the Formula to Find the Height of a Cylinder

Armed with the derived formula for the height of a cylinder in terms of its volume and radius, we are poised to embark on the practical application of this mathematical revelation. The formula, expressed as h = V / (πr^2), encapsulates the essence of the cylinder's height, offering a direct pathway to unveil this hidden dimension based solely on the known volume and radius.

To illustrate the practical application of this formula, let us consider a hypothetical scenario where we are presented with a cylindrical container of known volume and radius. Suppose the container possesses a volume of 100 cubic units and a radius of 5 units. By leveraging the derived formula, we can effortlessly determine the height of the cylinder, thus unraveling its concealed dimension with precision and mathematical finesse.

Substituting the given values into the formula, we obtain:

h = 100 / (π * 5^2)
= 100 / (25π)
≈ 100 / 78.54
≈ 1.27 units

Through this calculation, we unveil the height of the cylinder to be approximately 1.27 units. This exemplifies the practical potency of the formula, as it empowers us to discern the height of the cylinder with remarkable accuracy based solely on the provided volume and radius.

Furthermore, the application of this formula extends beyond mere calculation, transcending numerical values to embody the essence of geometric reasoning. It serves as a testament to the profound unity between the volumetric properties and geometric dimensions of the cylinder, illuminating the intrinsic relationship between its volume, radius, and height.

In a real-world context, the application of this formula holds immense practical significance, facilitating the precise determination of cylindrical dimensions in diverse fields such as engineering, architecture, and manufacturing. Whether it involves designing storage vessels, optimizing structural components, or engineering fluid systems, the ability to ascertain the height of a cylinder based on its volume and radius engenders a profound impact on the practical realm of geometric analysis and spatial reasoning.

As we witness the seamless application of the formula to unveil the height of a cylinder, we are reminded of the profound mathematical elegance that underpins this geometric revelation. It stands as a testament to the harmonious fusion of mathematical reasoning and geometric dimensions, offering a gateway to unravel the hidden depths of cylindrical forms with precision and clarity.

In essence, the application of the formula to find the height of a cylinder represents a triumph of mathematical reasoning, as it unveils the intrinsic relationship between the volume, radius, and height of the cylinder in a succinct and powerful expression. Through this practical demonstration, we embrace the profound implications of this formula in illuminating the hidden dimensions of cylinders, transcending numerical values to embody the geometric essence of these captivating shapes.

Conclusion

In conclusion, our journey through the captivating realm of cylinders has unveiled the profound interplay between their volumetric properties and geometric dimensions. We embarked on this mathematical odyssey with the singular quest of unraveling the height of a cylinder based solely on its volume and radius, delving into the essence of geometric reasoning and mathematical elegance. Through our exploration, we have gained a deep appreciation for the intrinsic relationship between the volume, radius, and height of a cylinder, culminating in the derivation and practical application of a formula that unlocks the hidden dimension of this three-dimensional shape.

The derived formula, expressed as h = V / (πr^2), stands as a testament to the profound unity between the volumetric properties and geometric dimensions of a cylinder. It transcends mere numerical values to embody the geometric essence of this captivating shape, offering a direct pathway to discern its concealed height with precision and mathematical finesse. This formula holds immense practical significance, extending beyond mere calculation to impact diverse fields such as engineering, architecture, and manufacturing. It empowers practitioners to ascertain cylindrical dimensions with remarkable accuracy, fostering advancements in geometric analysis and spatial reasoning.

As we reflect on our journey, we are reminded of the elegance and ingenuity that underpin the mathematical reasoning behind the height of a cylinder. This enigmatic quest has not only enriched our understanding of geometric forms but has also illuminated the profound implications of mathematical reasoning in unraveling the hidden dimensions of complex shapes. The allure of cylinders, with their enigmatic volumes and towering heights, has beckoned us to embrace the beauty of mathematical reasoning and the captivating interplay between dimensions and spatial magnitude.

In the grand tapestry of mathematical inquiry, our exploration into the height of a cylinder serves as a testament to the enduring allure of geometric puzzles and the timeless elegance of mathematical reasoning. It underscores the profound unity between abstract concepts and tangible dimensions, offering a glimpse into the harmonious fusion of logic, creativity, and spatial reasoning. As we conclude our journey, we carry with us the enduring legacy of mathematical discovery, empowered by the knowledge and insights gained from unraveling the enigma of finding the height of a cylinder based solely on its volume and radius.