Discover The Height And Volume Of A Triangular Pyramid With Mind-Blowing Precision!

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)

Introduction

Welcome to the fascinating world of triangular pyramids, where we unravel the secrets of their height and volume with mind-blowing precision! Triangular pyramids, also known as tetrahedrons, are three-dimensional geometric figures that possess a triangular base and three triangular faces that converge at a single point called the apex. These captivating structures have intrigued mathematicians, architects, and engineers for centuries due to their unique properties and applications in various fields.

In this article, we will embark on an illuminating journey to explore the intricacies of triangular pyramids, delving into their fundamental characteristics and unveiling the methods to determine their height and volume. By the end of our expedition, you will gain a profound understanding of these geometric marvels and the remarkable calculations involved in uncovering their essential dimensions.

Prepare to be captivated as we venture into the realm of triangular pyramids, where mathematical precision meets real-world significance. Let's embark on this exhilarating exploration and unravel the mysteries of triangular pyramids, unlocking their height and volume with unparalleled accuracy and insight.

Understanding Triangular Pyramids

Triangular pyramids, also known as tetrahedrons, are captivating three-dimensional geometric figures that boast a triangular base and three triangular faces that converge at a single point known as the apex. These structures possess a remarkable blend of elegance and complexity, making them a subject of fascination for mathematicians, architects, and enthusiasts of geometry.

The defining feature of a triangular pyramid is its base, which is a triangle, and its four faces, three of which are triangular and one that is the base. The three triangular faces extend from the base to the apex, creating a striking visual and structural composition. This unique arrangement sets triangular pyramids apart from other geometric forms, endowing them with distinctive properties and mathematical significance.

One of the key characteristics of triangular pyramids is their symmetry. The triangular base and the converging triangular faces exhibit symmetrical patterns, lending a sense of balance and harmony to these geometric wonders. This symmetrical arrangement not only contributes to the aesthetic appeal of triangular pyramids but also holds profound implications in mathematical calculations and spatial analysis.

Furthermore, triangular pyramids are renowned for their stability and structural integrity. The converging triangular faces culminate at the apex, forming a point of equilibrium that distributes the forces and pressures exerted on the pyramid. This structural stability has made triangular pyramids a subject of interest in architectural and engineering contexts, where their geometric properties are leveraged to design resilient and efficient structures.

In addition to their geometric allure, triangular pyramids play a pivotal role in the realm of spatial visualization and understanding. By studying and manipulating triangular pyramids, mathematicians and educators impart essential concepts of geometry and spatial reasoning to learners, fostering a deep understanding of three-dimensional forms and their interrelationships.

As we unravel the intricacies of triangular pyramids, we gain a profound appreciation for their geometric elegance and mathematical significance. These captivating structures serve as a testament to the beauty and complexity of geometric forms, inspiring a sense of wonder and curiosity in the realm of mathematics and beyond.

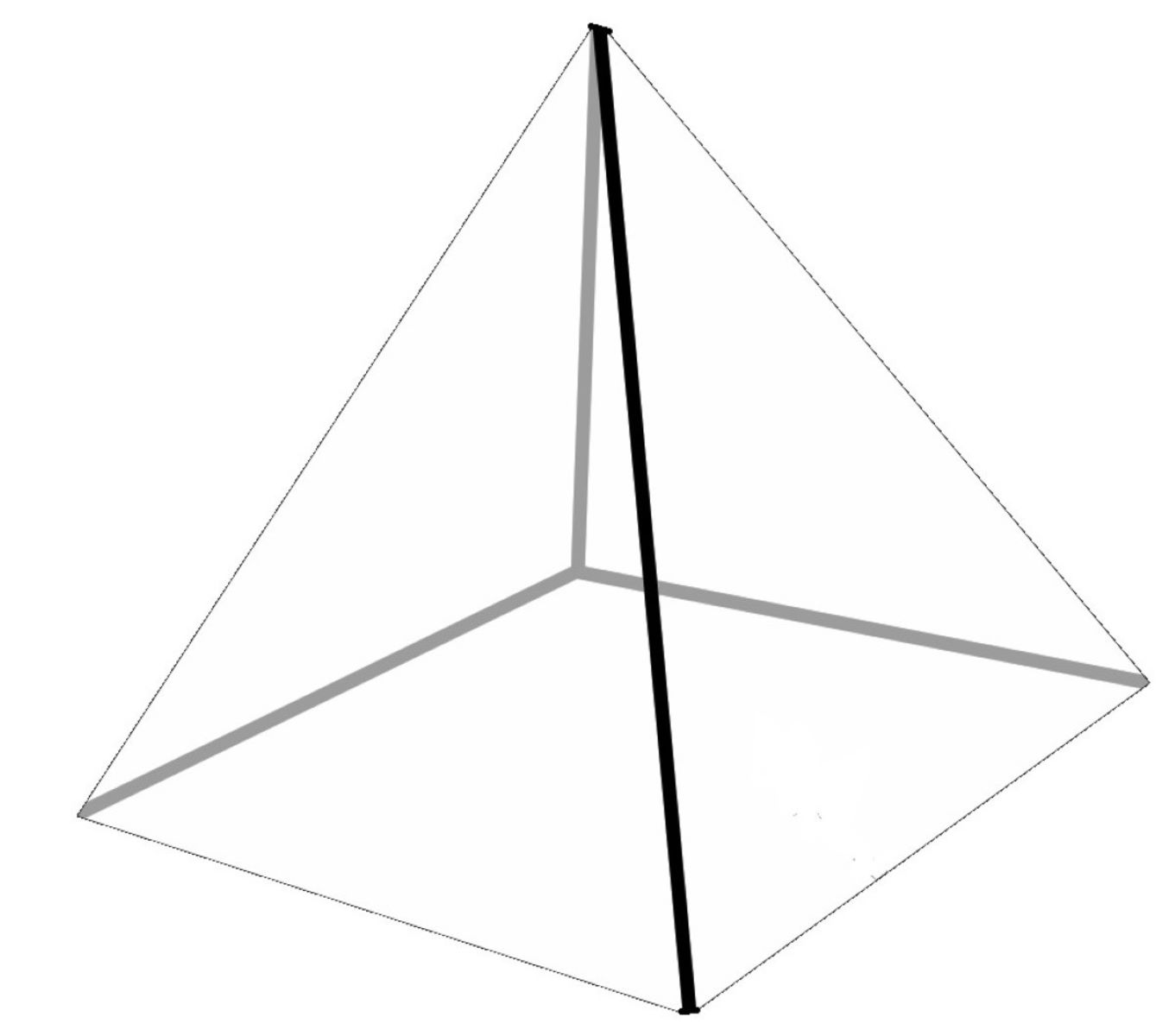
Finding the Height of a Triangular Pyramid

To determine the height of a triangular pyramid, we delve into the intricate relationship between the pyramid's base, its triangular faces, and the apex. The height of a triangular pyramid is a crucial dimension that not only contributes to its visual proportions but also holds significant implications in various mathematical and practical contexts.

The height of a triangular pyramid is perpendicular to its base and extends from the base to the apex, forming a vertical line that defines the pyramid's spatial orientation. To calculate this essential dimension, we rely on the geometric properties of the pyramid's base triangle and the relationships between its vertices and edges.

One method to find the height of a triangular pyramid involves leveraging the properties of similar triangles. By examining the cross-section of the pyramid that passes through the apex and is parallel to the base, we can identify a smaller triangle that shares proportional sides with the base triangle. This smaller triangle, formed by connecting the apex to the midpoints of the base triangle's edges, provides valuable insights into the pyramid's height.

Through the application of geometric principles and the concept of proportional sides, we can establish a relationship between the height of the triangular pyramid and the dimensions of the base triangle. This relationship enables us to derive the height with remarkable precision, unveiling the vertical extent of the pyramid in relation to its base and apex.

Another approach to finding the height of a triangular pyramid involves utilizing trigonometric functions and the angles formed by the pyramid's faces. By examining the angular relationships within the pyramid, particularly the angles between the base triangle and the adjacent triangular faces, we can employ trigonometric ratios to ascertain the height.

Furthermore, the height of a triangular pyramid plays a pivotal role in calculating its volume, as it directly influences the spatial capacity enclosed by the pyramid's base and faces. By accurately determining the height, we pave the way for precise volume calculations, unlocking the pyramid's three-dimensional magnitude with unparalleled accuracy.

In essence, the process of finding the height of a triangular pyramid encompasses a captivating exploration of geometric principles, spatial relationships, and mathematical techniques. Through a harmonious blend of analytical reasoning and geometric intuition, we unravel the height of these captivating structures, unveiling their vertical dimensions with breathtaking precision and insight.

Calculating the Volume of a Triangular Pyramid

Calculating the volume of a triangular pyramid is a captivating endeavor that involves unraveling the spatial capacity enclosed by its base and converging faces. The volume of a geometric figure represents the amount of space it occupies in three-dimensional space, making it a fundamental dimension with profound implications in mathematics, engineering, and real-world applications.

To embark on the journey of determining the volume of a triangular pyramid, we delve into the intricate relationships between its base triangle, height, and spatial extent. The formula for calculating the volume of a triangular pyramid is derived from the foundational principles of geometry and spatial analysis, offering a pathway to quantify the pyramid's three-dimensional magnitude with remarkable precision.

The formula for the volume of a triangular pyramid is expressed as V = (1/3) * B * h, where V represents the volume, B denotes the area of the base triangle, and h signifies the height of the pyramid. This elegant formula encapsulates the essence of the pyramid's spatial capacity, intertwining the dimensions of its base and height to unveil the volume with breathtaking clarity.

The process of calculating the volume of a triangular pyramid involves several captivating steps that showcase the interplay of geometric principles and mathematical reasoning. By first determining the area of the base triangle using established geometric formulas, such as the formula for the area of a triangle (A = 1/2 * base * height), we lay the foundation for the volume calculation.

Once the area of the base triangle is ascertained, we seamlessly integrate the height of the pyramid into the formula, harnessing its perpendicular relationship to the base to unveil the pyramid's volumetric magnitude. The height, a pivotal dimension in the volume calculation, influences the spatial extent enclosed by the pyramid, infusing the volume formula with a sense of vertical dimensionality and geometric significance.

As we harmoniously blend the area of the base triangle and the height within the volume formula, a symphony of geometric precision unfolds, culminating in the revelation of the triangular pyramid's volumetric capacity. This captivating process showcases the seamless integration of foundational geometric concepts and spatial analysis, illuminating the pyramid's volume with unparalleled clarity and insight.

In essence, the journey of calculating the volume of a triangular pyramid transcends mere mathematical computation, evolving into a captivating exploration of spatial dimensions and geometric elegance. By unraveling the pyramid's volumetric magnitude with precision and insight, we gain a profound appreciation for its three-dimensional essence and its significance in the realm of geometry and beyond.

Practical Applications of Triangular Pyramids

The captivating properties of triangular pyramids extend far beyond the realm of mathematical abstraction, finding practical applications in diverse fields ranging from architecture and engineering to physics and crystallography. These geometric marvels, with their distinctive triangular base and converging faces, serve as foundational elements in various structures and systems, harnessing their unique properties to fulfill essential functions and achieve remarkable efficiency.

In the realm of architecture and construction, triangular pyramids play a pivotal role in the design and construction of roofs, spires, and architectural elements that demand structural stability and aesthetic appeal. The inherent stability and equilibrium of triangular pyramids make them ideal candidates for supporting structures, where their geometric form distributes forces and pressures in a balanced manner, contributing to the resilience and longevity of architectural marvels.

Furthermore, in the field of engineering, triangular pyramids find applications in the design of trusses, support systems, and load-bearing structures, where their geometric properties are leveraged to optimize strength-to-weight ratios and enhance structural integrity. The symmetrical arrangement of triangular pyramids facilitates efficient load distribution and structural support, making them indispensable components in the construction of bridges, towers, and frameworks that demand robustness and reliability.

In the realm of physics and crystallography, the geometric properties of triangular pyramids manifest in the molecular and crystalline structures of various compounds and minerals. Triangular pyramids serve as fundamental motifs in crystal lattices, influencing the physical and chemical properties of crystals and contributing to their unique characteristics. The geometric arrangement of atoms or molecules in triangular pyramid formations underpins the behavior and properties of crystals, paving the way for diverse applications in materials science and industrial processes.

Moreover, in the realm of education and spatial visualization, triangular pyramids serve as invaluable tools for imparting geometric concepts and fostering a deep understanding of three-dimensional forms. Educators leverage the captivating nature of triangular pyramids to engage students in spatial reasoning, geometric analysis, and mathematical exploration, cultivating a profound appreciation for the elegance and significance of geometric forms in the realm of mathematics and beyond.

In essence, the practical applications of triangular pyramids span a diverse spectrum of disciplines, showcasing their versatility, stability, and geometric elegance in real-world contexts. From architectural marvels to molecular structures, triangular pyramids continue to inspire awe and admiration, leaving an indelible mark on the realms of mathematics, science, and engineering.

Conclusion

In conclusion, our exhilarating exploration into the realm of triangular pyramids has unveiled the captivating intricacies of these geometric marvels, shedding light on their fundamental properties and the methods to determine their height and volume with unparalleled precision. The journey through the symmetrical elegance of triangular pyramids has not only enriched our understanding of geometric forms but also highlighted their profound significance in diverse fields, from architecture and engineering to physics and crystallography.

As we reflect on the geometric allure and practical applications of triangular pyramids, we are reminded of their timeless relevance and enduring impact in the realms of mathematics and beyond. The symmetrical equilibrium and structural stability of triangular pyramids have made them indispensable elements in architectural and engineering marvels, where their geometric properties contribute to resilience, efficiency, and aesthetic appeal. Furthermore, the geometric motifs of triangular pyramids resonate in the molecular and crystalline structures of compounds and minerals, shaping the physical and chemical properties of crystals and influencing diverse applications in materials science and industrial processes.

Our exploration has also underscored the educational significance of triangular pyramids, serving as invaluable tools for imparting geometric concepts and nurturing spatial reasoning in learners. By engaging students in the captivating realm of triangular pyramids, educators foster a deep appreciation for geometric elegance and mathematical significance, instilling a sense of wonder and curiosity in the realm of mathematics and spatial visualization.

In essence, our journey through the realm of triangular pyramids has transcended mere mathematical exploration, evolving into a captivating odyssey that celebrates the elegance, symmetry, and practical relevance of these geometric wonders. As we conclude our expedition, we carry with us a profound appreciation for the timeless allure and enduring significance of triangular pyramids, inspiring a sense of wonder and curiosity that resonates in the realms of mathematics, science, and beyond.