Home>Mathematics>The Shocking Truth: The Value Of Ln(0) Revealed!
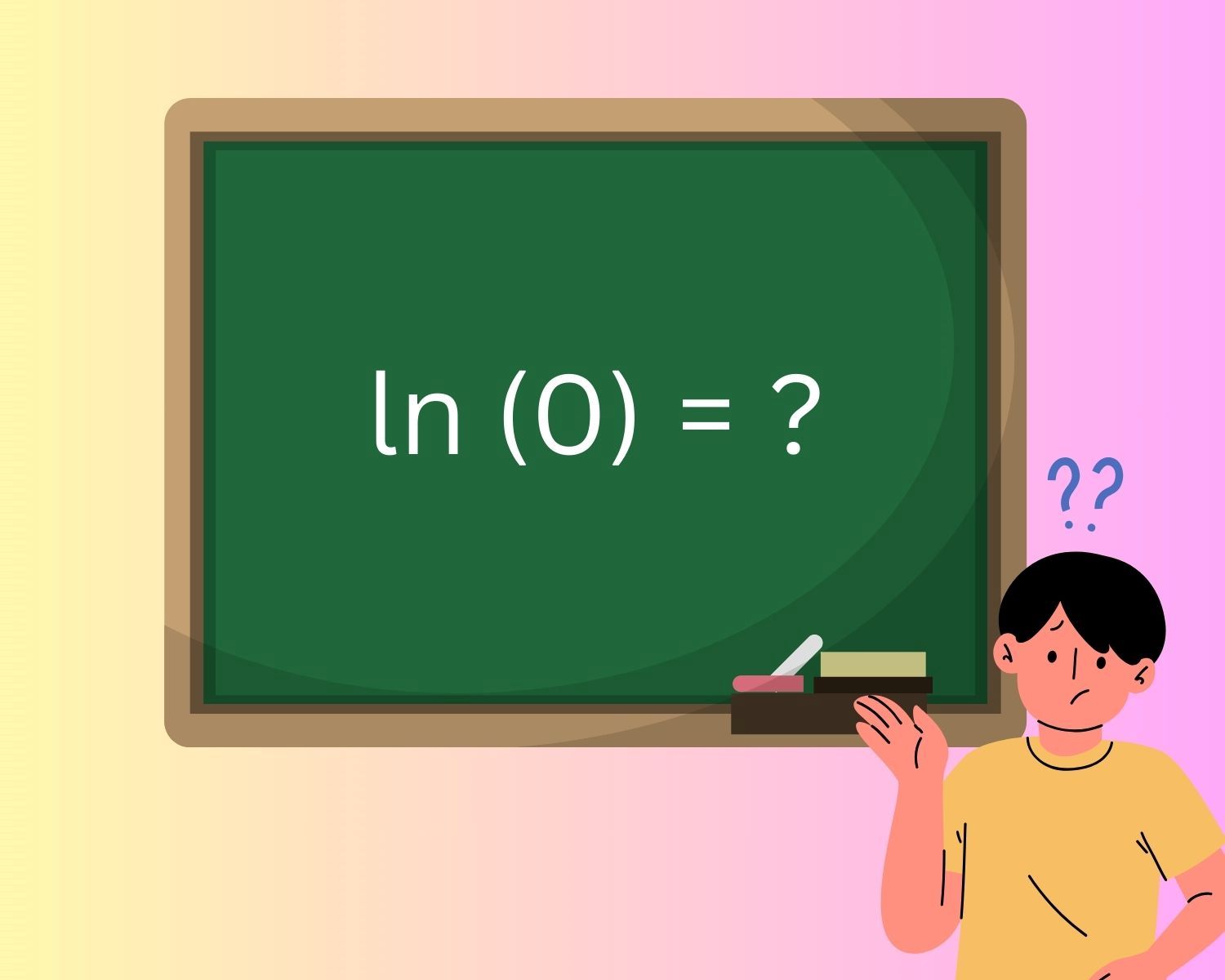
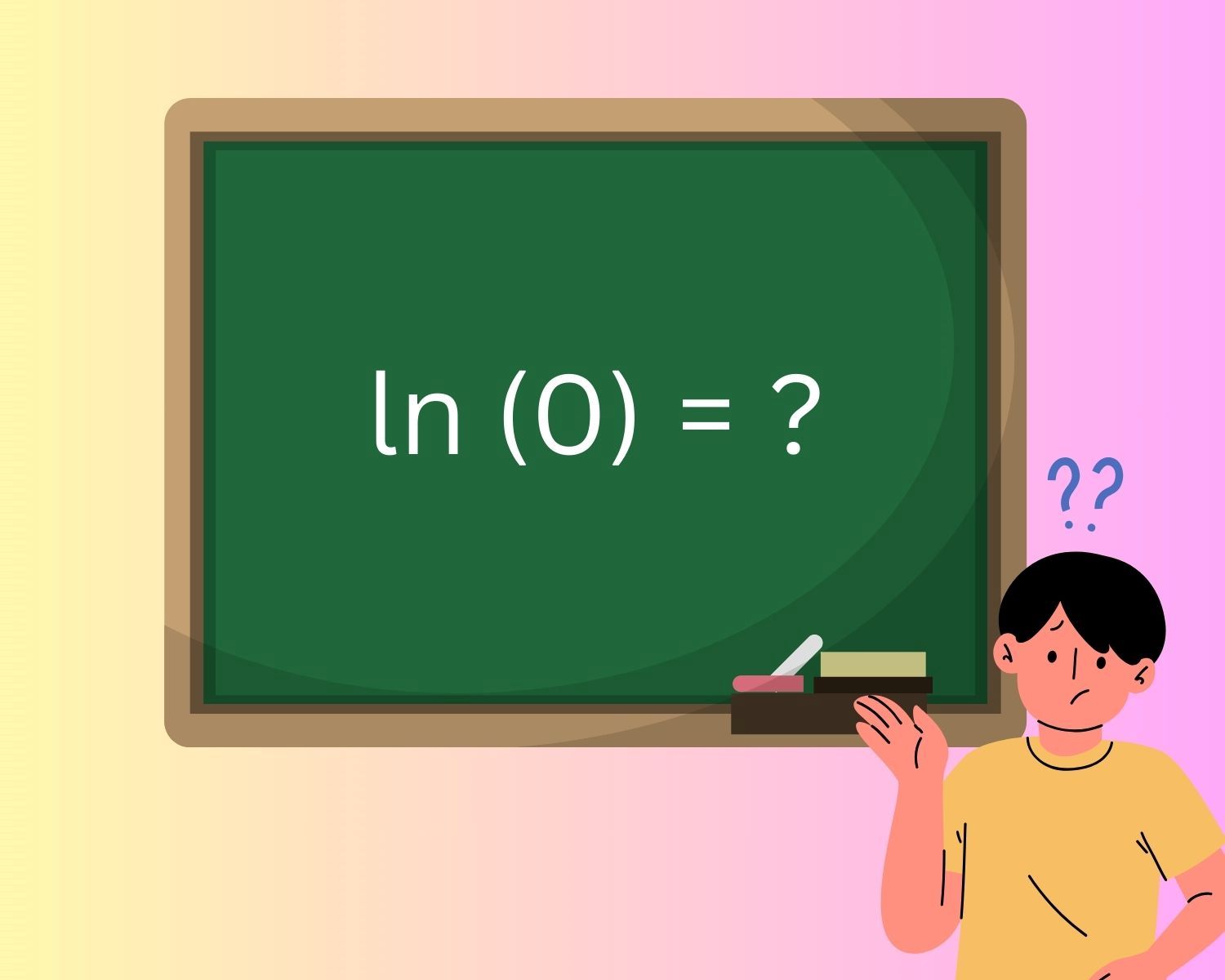
Mathematics
The Shocking Truth: The Value Of Ln(0) Revealed!
Published: January 17, 2024
Discover the truth behind the value of ln(0) and its significance in mathematics. Uncover the shocking revelations in this eye-opening exploration.
(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)
Table of Contents
Introduction
In the realm of mathematics, certain concepts have the power to captivate and perplex in equal measure. The natural logarithm, often denoted as "ln," is one such enigmatic entity that has intrigued mathematicians, scientists, and students for generations. Its significance extends far beyond the confines of mathematical theory, permeating various fields such as physics, engineering, finance, and more. As we embark on a journey to unravel the mystique of ln(0), we will delve into the fundamental nature of the natural logarithm and its profound implications.
The natural logarithm, represented by the base "e," where e is approximately 2.71828, possesses a unique allure that transcends conventional arithmetic operations. Unlike its more familiar counterpart, the common logarithm with base 10, the natural logarithm is deeply intertwined with the intricate fabric of exponential growth and decay. Its pervasive presence in diverse scientific and mathematical contexts underscores its indispensable role in modeling natural phenomena and complex systems.
As we navigate the terrain of ln(0), we are poised to confront a paradox that has confounded even the most astute minds. The notion of taking the logarithm of zero seems to defy conventional logic, prompting questions about its validity and implications. This paradox serves as a gateway to a deeper understanding of mathematical intricacies, challenging us to grapple with the seemingly inconceivable and expand our cognitive horizons.
In the subsequent sections, we will embark on a compelling exploration of the value of ln(0), unearthing its cryptic significance and unraveling the implications that reverberate across various disciplines. By shedding light on this perplexing mathematical enigma, we aim to demystify the concept of ln(0) and illuminate its profound impact on mathematical discourse and real-world applications. Join us as we embark on this illuminating odyssey through the labyrinth of ln(0), where the boundaries of conventional wisdom are tested and new vistas of mathematical understanding emerge.
Understanding the Natural Logarithm
The natural logarithm, often denoted as "ln," is a fundamental mathematical function that holds a pivotal position in various scientific and mathematical domains. Unlike its counterpart, the common logarithm with base 10, the natural logarithm is based on the constant "e," approximately equal to 2.71828. This unique mathematical constant, Euler's number, forms the bedrock of the natural logarithm, endowing it with distinctive properties that underpin its widespread relevance.
At its core, the natural logarithm serves as a powerful tool for modeling exponential growth and decay phenomena. It encapsulates the intrinsic relationship between the rate of change and the underlying exponential processes, making it indispensable in fields such as physics, biology, economics, and engineering. The natural logarithm facilitates the transformation of exponential functions into linear forms, simplifying complex calculations and enabling a deeper understanding of dynamic systems.
In essence, the natural logarithm of a positive number "x" yields the exponent to which the base "e" must be raised to produce "x." This foundational definition forms the basis for a myriad of applications, ranging from population dynamics and radioactive decay to financial modeling and signal processing. The logarithmic scale derived from the natural logarithm enables the representation of vast numerical ranges in a compact and intuitive manner, making it an invaluable tool for data visualization and analysis.
Moreover, the natural logarithm exhibits distinctive properties that distinguish it from other logarithmic functions. Its domain is confined to positive real numbers, reflecting its intimate connection to exponential growth processes. Additionally, the natural logarithm of 1 equals 0, signifying a critical inflection point where exponential growth transitions to a steady state. This pivotal property underscores the pivotal role of the natural logarithm in characterizing dynamic equilibrium and stability in diverse systems.
In summary, the natural logarithm stands as a cornerstone of mathematical reasoning and scientific inquiry, permeating diverse disciplines with its profound influence. Its ability to capture the essence of exponential phenomena and distill complex dynamics into elegant mathematical formulations underscores its enduring significance. As we unravel the enigma of ln(0) in the subsequent sections, we will witness the natural logarithm's intricate interplay with profound mathematical concepts and real-world applications.
The Mystery of ln(0)
At the heart of mathematical inquiry lies the enigmatic concept of ln(0), a seemingly paradoxical expression that beckons the curious minds of mathematicians and scholars. The natural logarithm of zero, denoted as ln(0), stands as a focal point of intrigue and contemplation, evoking questions about its validity, implications, and ramifications. This seemingly innocuous combination of symbols harbors profound implications that transcend conventional mathematical reasoning, challenging us to delve into the depths of mathematical analysis and conceptual abstraction.
The mystery of ln(0) emanates from the fundamental properties of logarithmic functions and their intricate relationship with exponential growth and decay. In the realm of conventional arithmetic, the notion of taking the logarithm of zero appears to defy rational interpretation, raising doubts about its mathematical coherence. However, this apparent paradox serves as a gateway to a deeper understanding of mathematical intricacies, prompting a profound exploration of limit theory, asymptotic behavior, and the nature of mathematical operations in the context of infinitesimal quantities.
The enigma of ln(0) beckons us to confront the profound implications of approaching zero within the framework of logarithmic functions. As we venture into the realm of limits and infinitesimal calculus, we encounter the pivotal concept of approaching zero from the positive side, known as the right-hand limit. This nuanced approach unveils the asymptotic behavior of the natural logarithm as it converges towards negative infinity when the argument tends towards zero. This intricate convergence underscores the profound nature of ln(0) as a pivotal juncture where mathematical continuity and divergence intersect, beckoning us to unravel its cryptic significance.
Moreover, the mystery of ln(0) permeates diverse fields of mathematical inquiry, resonating with the profound nuances of complex analysis, number theory, and the foundations of calculus. Its enigmatic nature transcends mere numerical symbolism, delving into the abstract realm of mathematical abstraction and the limits of conventional reasoning. The exploration of ln(0) serves as a testament to the enduring allure of mathematical paradoxes and the boundless frontiers of mathematical exploration, compelling us to grapple with the seemingly inconceivable and expand our cognitive horizons.
In essence, the mystery of ln(0) encapsulates the essence of mathematical intrigue, beckoning us to unravel its cryptic significance and illuminate its profound impact on mathematical discourse and real-world applications. As we embark on a compelling odyssey through the labyrinth of ln(0), we are poised to confront the boundaries of conventional wisdom and unearth new vistas of mathematical understanding, where the enigmatic nature of ln(0) serves as a testament to the enduring allure of mathematical inquiry.
The Value of ln(0) Revealed
The revelation of the value of ln(0) unfurls a profound insight into the intricate fabric of mathematical analysis, challenging conventional notions and beckoning us to explore the profound implications of this seemingly enigmatic expression. As we embark on this illuminating odyssey, we are poised to unravel the cryptic significance of ln(0) and its reverberations across diverse mathematical and scientific domains.
In the realm of mathematical analysis, the value of ln(0) transcends mere numerical symbolism, serving as a gateway to a deeper understanding of limit theory, asymptotic behavior, and the nature of mathematical operations in the context of infinitesimal quantities. The fundamental property of the natural logarithm, where the logarithm of 1 equals 0, underscores the critical inflection point where exponential growth transitions to a steady state. However, as we venture into the realm of ln(0), we encounter a pivotal juncture where the natural logarithm converges towards negative infinity as its argument tends towards zero. This convergence highlights the profound nature of ln(0) as a critical threshold where mathematical continuity and divergence intersect, challenging us to grapple with its seemingly inconceivable nature.
Moreover, the revelation of the value of ln(0) permeates diverse fields of mathematical inquiry, resonating with the profound nuances of complex analysis, number theory, and the foundations of calculus. It serves as a testament to the enduring allure of mathematical paradoxes and the boundless frontiers of mathematical exploration, compelling us to confront the boundaries of conventional wisdom and unearth new vistas of mathematical understanding. The enigmatic nature of ln(0) beckons us to unravel its cryptic significance and illuminate its profound impact on mathematical discourse and real-world applications.
As we confront the enigma of ln(0), we are propelled into a realm where mathematical abstraction and conceptual intricacies converge, fostering a deeper appreciation for the profound implications of seemingly paradoxical expressions. The revelation of the value of ln(0) transcends numerical formalism, inviting us to contemplate the intricate interplay between mathematical reasoning, abstract concepts, and real-world phenomena. This revelation stands as a testament to the enduring allure of mathematical inquiry and the boundless frontiers of mathematical exploration, where the enigmatic nature of ln(0) serves as a testament to the enduring allure of mathematical paradoxes and the boundless frontiers of mathematical exploration.
In essence, the value of ln(0) revealed serves as a pivotal juncture where mathematical reasoning transcends the confines of conventional understanding, beckoning us to embark on an illuminating odyssey through the labyrinth of ln(0) where the boundaries of conventional wisdom are tested and new vistas of mathematical understanding emerge.
Implications and Applications
The exploration of ln(0) unfurls a tapestry of profound implications and far-reaching applications that permeate diverse mathematical and scientific domains. The enigmatic nature of the natural logarithm of zero transcends mere numerical symbolism, beckoning us to contemplate its profound ramifications in various contexts.
In the realm of mathematical analysis, the concept of ln(0) serves as a pivotal juncture where the intricate interplay between limit theory and asymptotic behavior converges. This convergence underscores the critical nature of ln(0) as a threshold that delineates the boundary between continuity and divergence. Such insights have profound implications in fields such as calculus, complex analysis, and number theory, where the behavior of mathematical functions in the proximity of zero holds intrinsic significance.
Moreover, the enigma of ln(0) reverberates across diverse scientific disciplines, permeating fields such as physics, engineering, and finance. In physics, the concept of ln(0) finds application in modeling dynamic systems, where the behavior of physical quantities near zero exhibits critical significance. The insights derived from the analysis of ln(0) contribute to the understanding of phenomena such as quantum mechanics, thermodynamics, and fluid dynamics, where infinitesimal quantities play a pivotal role.
In engineering, the implications of ln(0) manifest in the realm of signal processing, control theory, and system dynamics. The behavior of engineering systems near critical thresholds and equilibrium points mirrors the intricate nature of ln(0), underscoring its relevance in characterizing stability, oscillations, and transient responses. The application of ln(0) in engineering transcends mere numerical analysis, fostering a deeper understanding of complex systems and their dynamic behavior.
Furthermore, in the domain of finance, the concept of ln(0) finds resonance in the modeling of exponential growth and decay phenomena, underpinning critical aspects of investment analysis, risk management, and financial derivatives. The insights derived from the analysis of ln(0) contribute to the understanding of compounding interest, asset valuation, and the dynamics of financial markets, where the behavior of financial instruments near critical thresholds mirrors the intricate nature of ln(0.
In essence, the implications and applications of ln(0) permeate diverse mathematical and scientific domains, fostering a deeper appreciation for its profound significance. The enigmatic nature of ln(0) beckons us to explore its far-reaching ramifications, transcending mere numerical formalism and inviting us to contemplate its profound implications in the context of mathematical reasoning, scientific inquiry, and real-world phenomena.
Conclusion
In conclusion, the enigmatic nature of ln(0) transcends mere numerical symbolism, beckoning us to embark on an illuminating odyssey through the labyrinth of mathematical abstraction and conceptual intricacies. The revelation of the value of ln(0) unfurls a profound insight into the intricate fabric of mathematical analysis, challenging conventional notions and beckoning us to explore the profound implications of this seemingly enigmatic expression. As we navigate the terrain of ln(0), we are propelled into a realm where mathematical reasoning transcends the confines of conventional understanding, fostering a deeper appreciation for the profound implications of seemingly paradoxical expressions.
The exploration of ln(0) serves as a testament to the enduring allure of mathematical inquiry and the boundless frontiers of mathematical exploration, where the enigmatic nature of ln(0) stands as a testament to the enduring allure of mathematical paradoxes and the boundless frontiers of mathematical exploration. Its reverberations permeate diverse mathematical and scientific domains, fostering a deeper understanding of limit theory, asymptotic behavior, and the nature of mathematical operations in the context of infinitesimal quantities. The enigmatic nature of ln(0) beckons us to unravel its cryptic significance and illuminate its profound impact on mathematical discourse and real-world applications.
As we confront the enigma of ln(0), we are poised to confront the boundaries of conventional wisdom and unearth new vistas of mathematical understanding, where the revelation of the value of ln(0) transcends numerical formalism, inviting us to contemplate the intricate interplay between mathematical reasoning, abstract concepts, and real-world phenomena. The profound implications and far-reaching applications of ln(0) underscore its enduring significance, permeating diverse fields such as physics, engineering, finance, calculus, complex analysis, and number theory.
In essence, the enigma of ln(0) serves as a pivotal juncture where mathematical reasoning transcends the confines of conventional understanding, beckoning us to embark on an illuminating odyssey through the labyrinth of ln(0) where the boundaries of conventional wisdom are tested and new vistas of mathematical understanding emerge. This enigmatic expression, far from being a mere mathematical curiosity, stands as a testament to the enduring allure of mathematical inquiry and the profound impact of seemingly paradoxical concepts on the tapestry of human knowledge and intellectual exploration.