Mind-Blowing Quadrilateral Revelation: Not All Four Congruent Sides Make A Square!

(Many of the links in this article redirect to a specific reviewed product. Your purchase of these products through affiliate links helps to generate commission for Regretless.com, at no extra cost. Learn more)

Introduction

Quadrilaterals, the four-sided wonders of geometry, have long fascinated mathematicians and students alike. From the familiar square to the more complex trapezoid and parallelogram, these shapes are fundamental to our understanding of geometry. However, there's a mind-blowing revelation that challenges our preconceived notions about quadrilaterals: Not all four congruent sides make a square!

In this article, we'll delve into the captivating world of quadrilaterals, exploring their properties and shedding light on the surprising revelation that not all quadrilaterals with four equal sides are squares. Prepare to embark on a journey that will transform the way you perceive these geometric marvels.

Let's unravel the mystery of quadrilaterals and uncover the hidden truths that lie within their four sides and angles. Are you ready to challenge your understanding of these fundamental shapes? Join us as we embark on this enlightening exploration of quadrilaterals and discover the unexpected secrets they hold.

Understanding Quadrilaterals

Quadrilaterals are polygons with four sides, making them a cornerstone of geometric study. These versatile shapes come in various forms, each possessing unique properties that distinguish them from one another. Understanding the defining characteristics of quadrilaterals is essential for navigating the intricate world of geometry.

One of the fundamental aspects of quadrilaterals is their diverse set of attributes, including side lengths, angle measures, and symmetry. These properties enable mathematicians and students to classify quadrilaterals into distinct categories, each with its own set of defining features.

Moreover, the interior angles of a quadrilateral play a crucial role in its classification. By examining the measures of these angles, we can determine the type of quadrilateral we are dealing with. From the right angles of a rectangle to the equal opposite angles of a parallelogram, these angle measures serve as valuable indicators of a quadrilateral's nature.

Furthermore, the concept of diagonals in quadrilaterals adds another layer of complexity to their study. Diagonals are line segments that connect non-adjacent vertices of a quadrilateral, creating new opportunities for exploration and analysis. By examining the properties of these diagonals, we can uncover additional insights into the nature of quadrilaterals.

In addition to their individual properties, quadrilaterals also exhibit a wide range of symmetrical and asymmetrical characteristics. This diversity allows for a rich tapestry of shapes, each with its own distinct allure and mathematical significance.

Understanding the intricate nuances of quadrilaterals is a captivating journey that unveils the beauty and complexity of these geometric wonders. By delving into their defining features, we gain a deeper appreciation for the intricacies of geometry and the remarkable diversity of quadrilaterals.

As we continue our exploration of quadrilaterals, we will unravel the surprising revelation that not all quadrilaterals with four congruent sides form a square. This eye-opening discovery challenges conventional assumptions and underscores the multifaceted nature of these geometric shapes.

Stay tuned as we delve deeper into the captivating world of quadrilaterals, uncovering the unexpected truths that redefine our understanding of these fundamental shapes.

The Definition of a Square

A square is a remarkable quadrilateral distinguished by its unique properties. Defined as a four-sided polygon with all sides of equal length and all interior angles measuring 90 degrees, the square embodies symmetry and balance. This pristine symmetry is a defining characteristic that sets the square apart from other quadrilaterals, endowing it with a sense of harmony and precision.

The equal side lengths of a square contribute to its uniformity, creating a shape that is perfectly balanced and visually captivating. Each side of the square is not only equal in length to its counterparts but also parallel, forming a shape that exudes stability and order. This uniformity is a testament to the square's geometric purity, making it a cornerstone of mathematical exploration and architectural design.

Furthermore, the interior angles of a square play a pivotal role in defining its essence. With all four angles measuring 90 degrees, the square embodies the essence of right angles, symbolizing perpendicularity and geometric integrity. This characteristic distinguishes the square as a symbol of precision and rationality, making it a fundamental element in the realm of geometry and spatial reasoning.

In addition to its symmetrical and angular properties, the square's diagonals further enhance its geometric allure. The diagonals of a square bisect each other at right angles, creating four congruent right-angled triangles within the square. This intriguing geometric relationship adds another layer of complexity to the square's structure, highlighting its interconnected and harmonious nature.

The defining features of a square, including its equal side lengths, right angles, and symmetrical diagonals, establish it as a quintessential representation of geometric perfection. Its pristine form and balanced proportions make the square a symbol of order and precision, permeating various facets of human creativity and mathematical inquiry.

As we delve deeper into the world of quadrilaterals, the profound significance of the square's defining characteristics becomes increasingly apparent. The square stands as a testament to the inherent beauty and mathematical elegance embedded within geometric shapes, inspiring awe and admiration as a symbol of geometric harmony and balance.

The Mind-Blowing Revelation

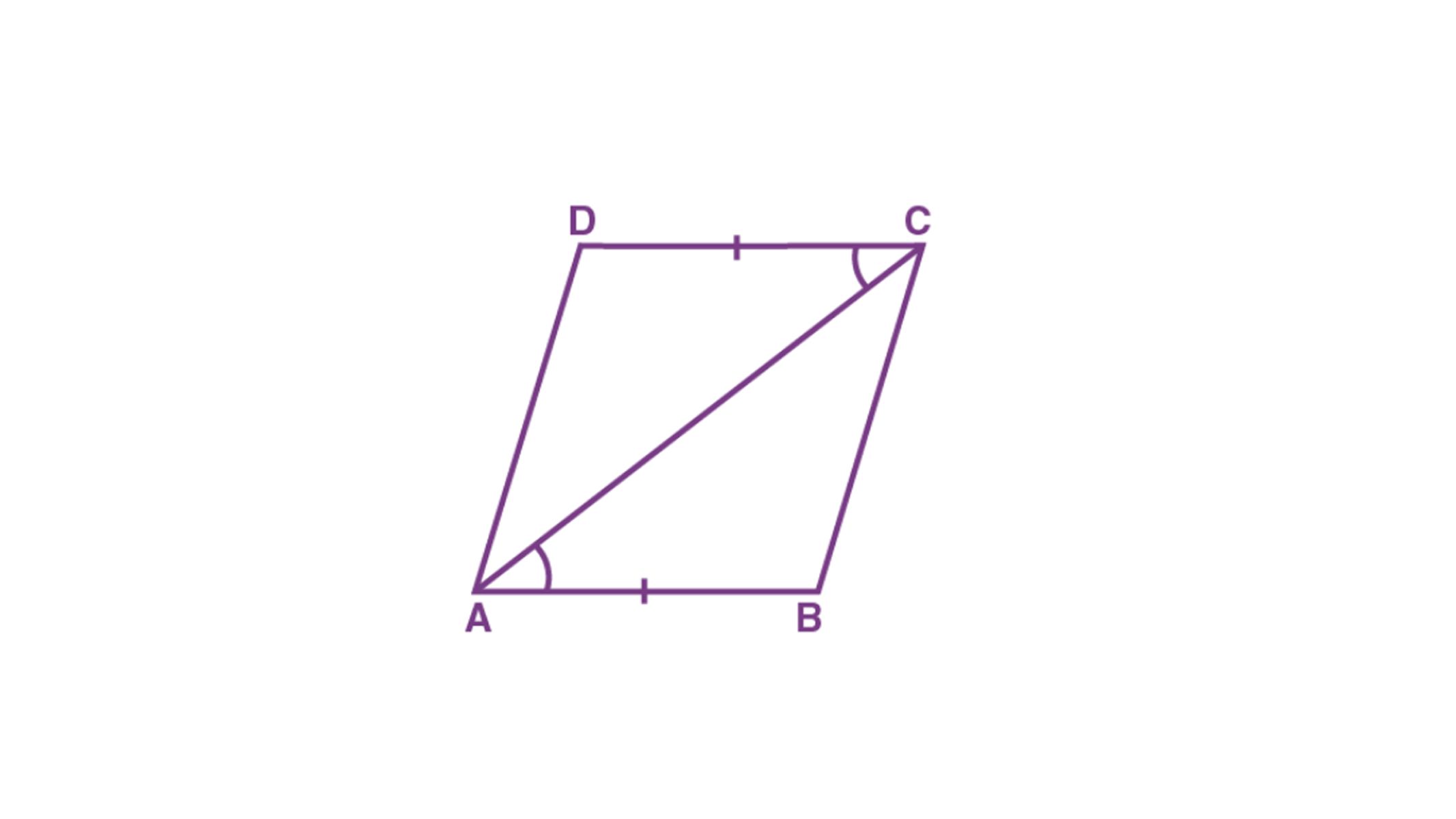
Amidst the intricate tapestry of quadrilaterals lies a revelation that defies conventional wisdom: not all quadrilaterals with four congruent sides form a square. This astonishing realization challenges our preconceived notions and unveils the multifaceted nature of these geometric marvels.

Traditionally, the notion that four equal sides unequivocally define a square has been deeply ingrained in mathematical discourse. However, this revelation shatters this long-standing assumption, prompting a reevaluation of our understanding of quadrilaterals.

The crux of this revelation lies in the recognition that while a square possesses four congruent sides, not all quadrilaterals with this characteristic exhibit the defining properties of a square. This pivotal insight underscores the nuanced interplay of side lengths, angle measures, and symmetry within quadrilaterals, revealing the intricate web of geometric relationships that govern their classification.

By unraveling this revelation, we gain a deeper appreciation for the complexity and diversity inherent in quadrilaterals. It compels us to explore the subtle distinctions that set squares apart from other four-sided shapes, fostering a deeper understanding of the intricate interplay of geometric properties.

This revelation serves as a catalyst for a paradigm shift in our perception of quadrilaterals, urging us to approach these shapes with a discerning eye and a willingness to embrace the unexpected. It highlights the dynamic nature of mathematical inquiry, where long-held assumptions are continually challenged and redefined, leading to new insights and revelations.

As we confront this mind-blowing revelation, we are reminded of the boundless nature of mathematical exploration and the perpetual sense of wonder it evokes. It beckons us to embark on a journey of discovery, where the familiar is reexamined, and the unknown is embraced with curiosity and fascination.

In the wake of this revelation, the world of quadrilaterals is imbued with newfound intrigue and complexity, inviting us to delve deeper into their enigmatic properties and unravel the hidden truths that redefine our perception of these fundamental shapes.

Examples of Non-Square Quadrilaterals

1. Rectangle: The rectangle, a classic non-square quadrilateral, shares certain similarities with the square, such as having four right angles. However, unlike the square, the rectangle does not possess equal side lengths. Its opposing sides are equal and parallel, contributing to its distinctive geometric properties. This asymmetry sets the rectangle apart from the perfect symmetry of the square, showcasing the diverse nature of quadrilaterals.

2. Rhombus: Another captivating non-square quadrilateral is the rhombus, which exhibits an intriguing blend of symmetry and asymmetry. With all sides of equal length, the rhombus embodies a sense of uniformity, akin to the square. However, its angles are not right angles, introducing a fascinating departure from the square's angular precision. This unique combination of equal sides and non-right angles distinguishes the rhombus as a captivating non-square quadrilateral.

3. Trapezoid: The trapezoid, characterized by a pair of parallel sides, offers a compelling contrast to the square's symmetrical allure. Its asymmetrical nature, defined by one pair of parallel sides and non-parallel sides, underscores the diverse array of quadrilaterals. The trapezoid's distinctiveness lies in its asymmetry, presenting a departure from the balanced proportions of the square and showcasing the rich variety of quadrilateral shapes.

4. Parallelogram: The parallelogram, with its opposite sides being parallel and equal in length, presents a captivating non-square quadrilateral. While it shares certain characteristics with the square, such as parallel sides, its lack of right angles sets it apart. This departure from the square's defining feature highlights the intricate differences that exist within the realm of quadrilaterals, underscoring the multifaceted nature of these geometric shapes.

5. Kite: The kite, with its unique configuration of two distinct pairs of adjacent sides, offers an unconventional yet captivating example of a non-square quadrilateral. Its asymmetrical nature, characterized by unequal adjacent sides, deviates from the uniformity of the square, providing a striking illustration of the diverse forms that quadrilaterals can assume.

As we explore these non-square quadrilaterals, we gain a deeper understanding of the remarkable diversity and complexity that permeate the world of geometric shapes. Each of these examples serves as a testament to the intricate interplay of side lengths, angles, and symmetry, underscoring the captivating nature of quadrilaterals and the profound insights they offer into the realm of geometry.

Conclusion

In conclusion, the captivating world of quadrilaterals encompasses a rich tapestry of shapes, each with its own unique properties and defining characteristics. Our exploration has unveiled the profound diversity and complexity that permeate the realm of geometric shapes, challenging conventional assumptions and redefining our understanding of these fundamental forms.

The mind-blowing revelation that not all quadrilaterals with four congruent sides form a square has reshaped our perception of these geometric marvels. This paradigm-shifting insight underscores the intricate interplay of side lengths, angle measures, and symmetry within quadrilaterals, inviting us to embrace the multifaceted nature of these shapes with curiosity and discernment.

As we reflect on the defining features of a square, including its equal side lengths, right angles, and symmetrical diagonals, we are reminded of the geometric perfection embodied by this iconic shape. The square stands as a testament to the inherent beauty and mathematical elegance embedded within geometric shapes, inspiring awe and admiration as a symbol of geometric harmony and balance.

Furthermore, our exploration of non-square quadrilaterals, such as the rectangle, rhombus, trapezoid, parallelogram, and kite, has illuminated the remarkable diversity and complexity that characterize these shapes. Each example serves as a testament to the intricate interplay of side lengths, angles, and symmetry, underscoring the captivating nature of quadrilaterals and the profound insights they offer into the realm of geometry.

This journey through the world of quadrilaterals has not only expanded our understanding of geometric shapes but has also highlighted the dynamic nature of mathematical inquiry. It underscores the perpetual sense of wonder and discovery that accompanies the exploration of mathematical concepts, challenging us to approach familiar notions with fresh perspectives and an openness to unexpected revelations.

As we embrace the multifaceted nature of quadrilaterals, we are reminded of the boundless opportunities for exploration and discovery that await within the realm of geometry. The intricate relationships and diverse properties of quadrilaterals invite us to delve deeper into their enigmatic nature, fostering a deeper appreciation for the beauty and complexity that define these fundamental shapes.

In essence, the revelation that not all four congruent sides make a square serves as a poignant reminder of the ever-evolving nature of mathematical inquiry. It encourages us to approach geometric concepts with a spirit of inquiry and a willingness to challenge conventional assumptions, paving the way for new revelations and a deeper understanding of the captivating world of quadrilaterals.